Dígito de control – Detección de errores

El “Dígito de control” o “Dígito verificador” es tipo de código Hash (tienes más información sobre códigos Hash aquí) muy sencillo que sirve para detectar errores (Existen otros que los corrigen, como el código Hamming). De este modo, si por ejemplo enviamos por Internet con nuestro ordenador/Smartphone/Tablet cualquier fichero (como pudiera ser una imagen) a un amigo, el dispositivo de nuestro amigo será capaz de deducir si los bits que componen al fichero le han llegado correctamente o no (por ejemplo, puede que una tormenta electromagnética modificara algunos bits por el camino; por tanto, no llegaría correctamente).

El Dígito de control se utiliza en muchos sitios, muchos más de los que seguramente imaginas. Donde seguramente lo has visto es en los números de las tarjetas de crédito, en el número del DNI (Documentos Nacional de Identidad); también aparece en otros, como en códigos de barras, números de facturas, números de identificación como de matrículas, ISBN, etc. En resumen, el dígito de control aparece en casi todos los papeles o tarjetas legales que ofrecen el gobierno, los bancos, o las tiendas; en el número que aparece como identificador.

Generalmente este dígito de control se calcula con el módulo elegido (elegido por el fabricante de la máquina que lee los códigos de barras, el gobierno que emite el DNI, el banco que emite la tarjeta, etc). Indicar que dependiendo del fabricante pudieran existir otras variantes sin utilizar el módulo.

Sobre todo, es muy interesante entender como calcular el módulo (que sirve para muchas cosas y es muy sencillo. Si nunca has visto o entendido del todo el módulo, pudieramos pensar que es algo complicado, pero muy al contrario la siguiente pregunta te resolverá su dificultad: ¿Sabes dividir? Si la respuesta es que sí, tener soltura con el módulo no te va a suponer un esfuerzo mayor a dividir), por eso hago un inciso para explicarlo (Nota sobre los ejemplos: los ejemplos son básicos para que todos puedan entender el artículo de una manera sencilla, si algo ya lo conoces simplemente puedes saltártelo o repasarlo; esto no quita que explique también cosas complejas desde lo básico).

¿Qué es el módulo (mod)?

Simplemente es el resto de la división entera (“división entera”, quiere decir que no va a haber decimales como “7,5”). Por ejemplo:

Sin resto (lo mismo que decir que el resto es cero “0”): 8 entre 2 es igual a 4, y su resto es 0 (en ejemplo simple, si tengo 8 caramelos y los reparto entre 2 niños, le toca 4 caramelos a cada niño, y sobran 0 caramelos sin repartir). En este caso el módulo (el resto) es 0. Dicho de otro modo, es “8 / 2 = 4” y “8 mod 2 = 0”
Con resto: 11 entre 4 es igual a 2 (sino fuera “división entera” el resultado hubiese sido “2,75” y con decimales nunca hay resto; por eso se usa la “división entera”, para que haya resto), y su resto es 3 (es decir, multiplicar el resultado de 2 por 4, y ver cuánto le falta hasta 11, por lo que 11 – 8 = 3; o en el ejemplo simple, 11 caramelos repartidos entre los 4 niños, le tocan 2 caramelos a cada niño, y sobran 3 sin repartir). En este caso el módulo (el resto) es 3. Dicho de otro modo, es “11 / 4 = 2” y “11 mod 4 = 3”

Se suele representar de dos maneras (que se leen “El módulo de Y de X es Z”; por ejemplo “El módulo 4 de 11 es 3”):

“X mod Y = Z” (ejemplo, “11 mod 4 = 3”)
“X % Y = Z” (ejemplo, “11 % 4 = 3”)

La gracia del módulo es que calcular “11 mod 4 = X” es sencillo “X” es “3”. Pero del resultado (el resto) “3” hallar por ejemplo “Y mod 4” la “Y” es complicado (por no decir imposible, ya que para “Y mod 4 = 3” también cumple “3 mod 4 = 3” o “7 mod 4 = 3” entre una infinidad de resultados posibles, y el que queríamos era “11”; por lo que podemos decir que no se puede deshacer el cálculo). De ahí la gracia de utilizar el módulo tantas veces para algoritmos de seguridad, pues incluso un ordenador tarda en calcularlo, ya que no es un cálculo directo 🙂

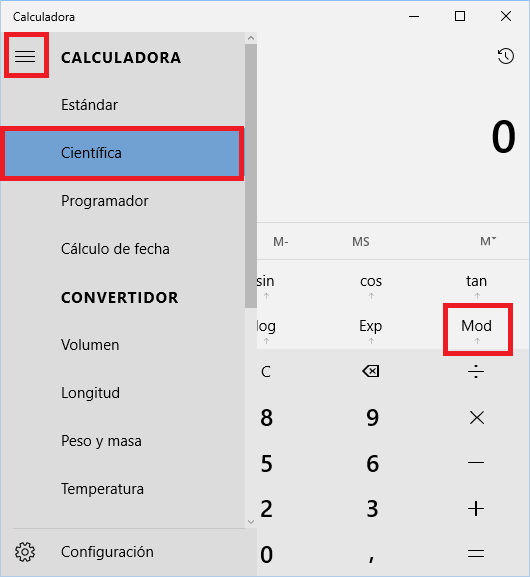
El módulo lo puedes calcular fácilmente con cualquier calculadora científica.

Por ejemplo, la calculadora de Windows si le pones el modo científico aparecerá la tecla “Mod”; para usarlo simplemente introduce el primer número, pulsa “Mod”, introduce el segundo número, y pulsa “=”.

En programación, el módulo es muy útil para calcular “repeticiones”, consumiendo los mínimos recursos y escribiendo las menos líneas de código. Pues con lo que hagamos el módulo será el último número y se repetirá.

Un ejemplo, imagina que tienes un listado con filas numeradas (como 1, 2, 3, 4, 5, 6, 7, …) y quieres que cada fila se colore primero con el color rojo, luego con el verde y por último con el azul, así repetidamente de manera infinita. Pues como tenemos tres colores podemos poner “F mod 3” donde “F” es el número de la fila, y el resultado de esta operación corresponderá “1” para el rojo, “2” para el verde y “0” para el azul (“1 mod 3 = 1”, “2 mod 3 = 2”, “3 mod 3 = 0”, “4 mod 3 = 1”, “5 mod 3 = 2”, “6 mod 3 = 0”, “7 mod 3 = 1”, …). Tendríamos un precioso listado coloreado con los mismos colores repetidos en el orden deseado 🙂

Otro ejemplo sería para deducir si es par o impar (por ejemplo, el número de la fila del listado anterior), con “F mod 2”, siendo el resultado “1” para impares y “0” para pares (“1 mod 2 = 1”, “2 mod 2 = 0”, “3 mod 2 = 1”, “4 mod 2 = 0”, “5 mod 2 = 1”, “6 mod 2 = 0”, “7 mod 2 = 1”, …).

Bit de Paridad

Se utiliza muchísimo para grupos de bits.

Lo voy a explicar rápidamente de una manera visual, luego entro en detalles (aunque es lo mismo pero un poco más técnico).

Supón que quieres enviar un mensaje en binario a tu amigo (binario que convertido a lenguaje humano podría significar algo, pero para este ejemplo no me interesa lo que signifique, sino si lo que envió es lo mismo que se recibe). El mensaje para el ejemplo (y cómo puedes ver en la siguiente imagen) va a ser “110110”

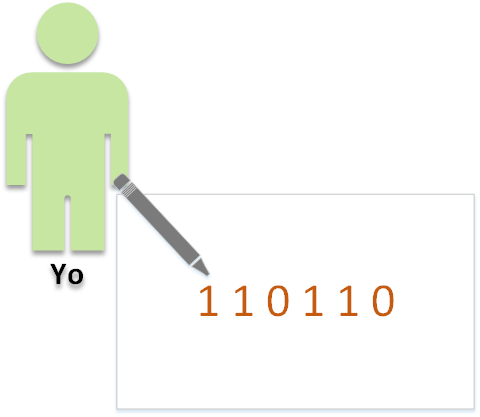Sabes que por el camino puede llegar erróneo así que decides añadir un “bit de paridad”. Un “bit de paridad” no es otra cosa más que contar los “unos” (“1s”) del mensaje, y cuyo resultado si es:

Si Par lo representaremos como 0
Si Impar lo representaremos como 1

¿Y por qué no al revés, el 1 como Par y el 0 como Impar? Paciencia, lo veremos unas pocas líneas más adelante.

Así que en el anterior ejemplo teníamos el mensaje “110110”, que contando el número de “1s” vemos que son “4”. Sabemos que el número “4” es un número par, así que escribimos un bit más (el bit de paridad) que va a ser el “0”. Por lo que lo que vamos a enviar va a ser “110110 0” (separo el bit de paridad para que se lea cómodo; si son bits eléctricos no hay separación ninguna, se envían uno tras otro, y ya el destino sabrá que el último bit es de paridad y el resto del mensaje).

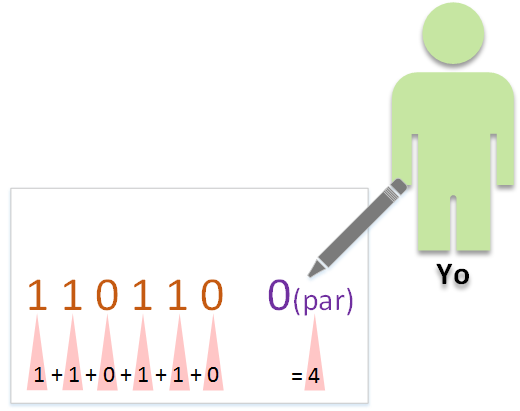Ya estamos preparados para enviar el mensaje a nuestro amigo. Por pasos (ir viendo la imagen siguiente en cada paso):

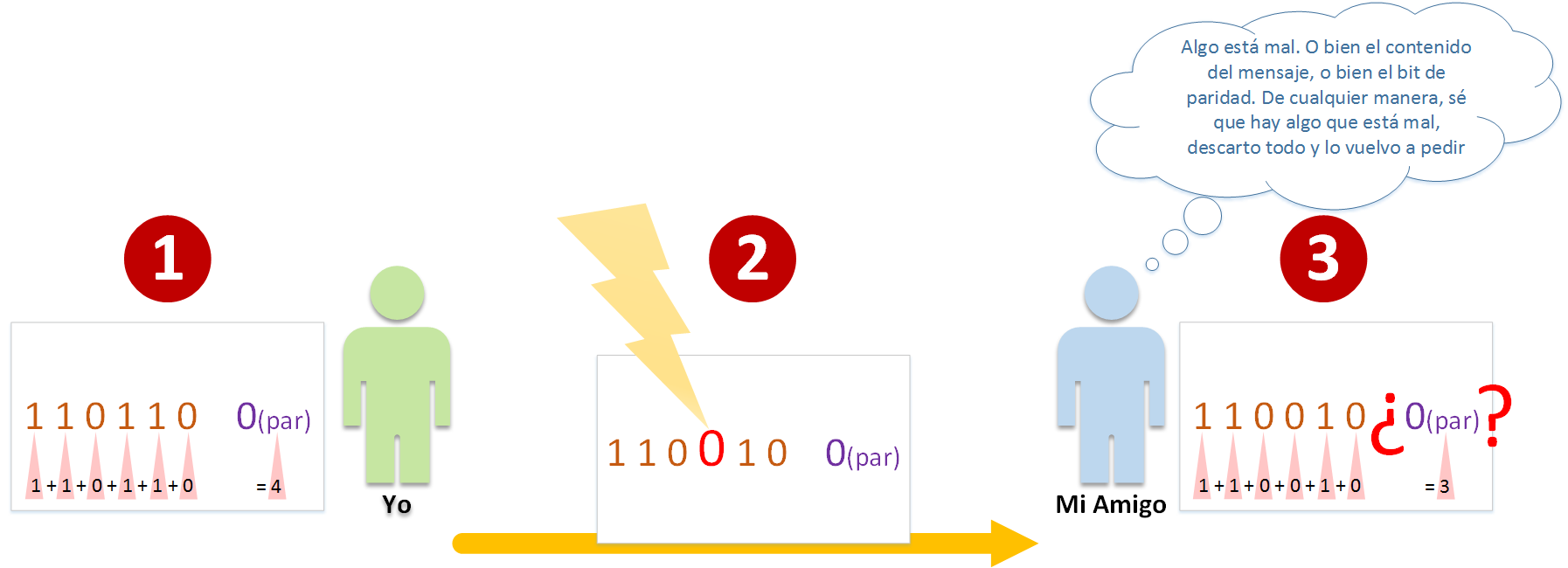
Escribo el mensaje (contenido del mensaje más el bit de paridad) a enviar a mi amigo (como acabamos de hacer), y lo envío.
Por el camino puede que haya algo que cambie el contenido del envío (si suponemos que se envía por un cable, una tormenta magnética podría cambiar algún dato por ejemplo; si te lo estabas imaginando como una carta, supón que la tormenta de agua emborrona tanto algún número del mensaje que lo cambia 😉 ). Podría no pasar nada por el camino y llegar de manera correcta, pero en este ejemplo vamos a hacer que ocurra algo inesperado, por lo que para el ejemplo se va a cambiar un 1 por un 0 quedando el mensaje de ejemplo: “110010 0”
Ahora nuestro amigo recibe el mensaje. Hace lo mismo, suma los “1s” del mensaje (sin sumar el bit de paridad); y ve que le da “3” de resultado, un número impar, por lo que si lo convertimos a bit de paridad debería de ser “1”. El bit de paridad recibido era 0 (indica “par”), y el procesado es “1” (indica “impar”), por lo que hay algo mal. En este punto no sabremos qué es lo que hay mal (si el mensaje o el bit de paridad), tampoco sabremos qué número de todos es el que es erróneo (o si hay varios que están mal). Lo que sí sabemos es que hay algo mal, por lo que nuestro amigo desechará el mensaje y lo volverá a pedir

¿Y si en el envío se cambian varios números de tal manera que la suma de “1s” por parte de nuestro amigo le dé un resultado también “par”?

Pues no podría detectar que ha habido un error y entendería el mensaje como válido. Indicar que esta manera evita muchos errores (si piensas en las infinitas posibilidades que existen, detecta muchos casos de error; no puedo decir la mitad exacta pues depende del azar, pero se acercará.

Y el resto de casos llegará el mensaje bien, por lo que tenemos más casos de éxito que de error contando con las veces pedidas de nuevo el mensaje al detectar el error). El “bit de paridad” es una de las maneras más simples, que consume menos recursos (da igual la potencia del procesador, se calcula en nada de tiempo) y menos memoria ocupa (1 bit).

Existen maneras que detectan muchos más casos de error, pero no tan optimas como el “bit de paridad” (aun así, todos los algoritmos de detección de errores tienen un máximo de bits erróneos que puede detectar como erróneos; la única manera de tener la absoluta certeza de que llega bien el mensaje es enviando el mismo mensaje infinitas veces al receptor para que lo compare infinitamente y asegurar al 100% que no ha habido error, cosa que no es para nada óptima).

La gracia del “bit de paridad” es que se suele utilizar como primera comprobación de grupos de bits, luego los grupos de bits (bien agrupados en otros grupos mayores, o bien en conjunto para formar el archivo), se vuelven a comprobar con otros algoritmos (como el código de Hamming, MD5 o SHA1, información más completa en el artículo de códigos Hash); así que resulta muy complicado que nuestro amigo no reciba sus datos de manera correcta, puede que después de pedir varios grupos de bits (o el archivo entero, que agrupa muchos grupos de bits, si es necesario), pero tendrá sus datos correctos con una alta probabilidad.

Calcular el bit de paridad con el módulo

Entendiendo como funciona el módulo es muy sencillo calcularlo de una forma un poco más técnica.

Simplemente se hace el módulo de 2 (“X mod 2”), y dependiendo del resultado será (aquí respondo a la pregunta anterior “¿Y por qué no al revés, el 1 como Par y el 0 como Impar?”, por el resultado que arroja el módulo de 2):

Si 0 será un número Par
Si 1 será un número Impar

Veamos el funcionamiento con un ejemplo (pongo el siguiente ejemplo pues para redes se suele utilizar algo muy parecido).

¿Recuerdas el ejemplo del principio del artículo, el de enviar un fichero a un amigo? pues ese fichero que queremos enviar se compone de bits, y esos bits se pueden dividir en grupos. Supongamos que nuestro fichero es:

Fichero competo en bits (los bits para un ordenador van sin espacios, los espacios los pongo para que se lea mejor): 1011 1010 1111

Lo podemos dividir en varios grupos:

Grupo A: 1011
Grupo B: 1010
Grupo C: 1111

La suma de 1s será nuestro bit de paridad:

Grupo A: 1011 tiene 3 1s, como 3 mod 2 = 1, por lo que el “Bit de paridad” es 1
Grupo B: 1010 tiene 2 1s, como 2 mod 2 = 0, por lo que el “Bit de paridad” es 0
Grupo C: 1111 tiene 4 1s, como 4 mod 2 = 0, por lo que el “Bit de paridad” es 0

De este modo podemos añadirlo al final de cada grupo de bts:

Grupo A: 10111
Grupo B: 10100
Grupo C: 11110

Y enviamos uno a uno cada grupo de bits a nuestro amigo. Si recibe alguno mal nos lo volverá a pedir. Lo calcula sin contar con el “Bit de paridad”, al final comparará el “Bit de paridad” recibido con el calculado para ver si está correcto. Supongamos que en el Grupo A le llega mal un bit que compone al fichero, el Grupo B recibe mal justo el «bit de paridad» y el Grupo C le llega correcto:

Grupo A: 00111. 0011 tiene 2 1s, como 2 mod 2 = 0, por lo que el “Bit de paridad” tendría que ser 0
Grupo B: 10101. 1010 tiene 2 1s, como 2 mod 2 = 0, por lo que el “Bit de paridad” tendría que ser 0
Grupo C: 11110. 1111 tiene 4 1s, como 2 mod 4 = 0, por lo que el “Bit de paridad” tendría que ser 0

Da igual que bit del grupo estuviera mal (si lo era el “Bit de paridad” o los bits que componen el fichero). En cuanto haya algo que no cuadre se detecta como erróneo (y habría que volver a pedir esos grupos de bits). De lo anterior podemos entonces deducir que:

Grupo A: 00111. El “Bit de paridad” recibido es 1 diferente al calculado que es 0. Grupo con Error
Grupo B: 10101. El “Bit de paridad” recibido es 1 diferente al calculado que es 0. Grupo con Error
Grupo C: 11110. El “Bit de paridad” recibido es 0 igual al calculado que es 0. Grupo Correcto

En el caso de que todos los grupos estuvieran bien, entonces se reconstruirá el fichero con todos los grupos de bits y nuestro amigo podrá utilizar el fichero (que probablemente sería alguna imagen o vídeo de gatitos, así que todo este trabajo matemático para que nuestro amigo vea gatitos 😀 ).

Calcular el bit de paridad con XOR

De esta manera se suele utilizar el «bit de paridad» como “Checksum”, pues calcular con el operador XOR a bajo nivel no consume muy poco tiempo de procesador.

Otra de las razones por la que se eligió que la suma de los 1s del Mensaje si es impar fuera «1» o par fuera «0» es precisamente porque al utilizar el operador «XOR» para obtener la paridad se obtienen las siguientes posibles y únicas salidas:

1 XOR 1 = 0
1 XOR 0 = 1
0 XOR 1 = 1
0 XOR 0 = 0

Así pues por ejemplo para los grupos anteriores de bits:

Grupo A: 1011
Grupo B: 1010
Grupo C: 1111

El procesador del ordenador calcularía el bit de paridad como:

Grupo A: 1011 -> (1 XOR 0) XOR (1 XOR 1) = 1 XOR 0 = 1.
Grupo B: 1010 -> (1 XOR 0) XOR (1 XOR 0) = 1 XOR 1 = 0.
Grupo C: 1111 -> (1 XOR 1) XOR (1 XOR 1) = 0 XOR 0 = 0.

E igual que con el módulo de 2, obtenemos el mismo resultado. Podemos añadir el bit de paridad calculado al final de cada grupo:

Grupo A: 10111
Grupo B: 10100
Grupo C: 11110

El resto se hace igual, salvo que ahora en vez de utilizar el módulo como hicimos antes, utilizamos el operador XOR (que es mucho más óptimo en consumo de memoria y de proceso).

Tarjetas de crédito o débito

En las tarjetas bancarias (da igual cual, si de crédito, débito, cuenta bancaria, etc) el “dígito de control” es el último dígito de los números que componen el “Número de la tarjeta” (es el número largo que está en la parte delantera de la tarjeta; que suele tener entre 12 a 19 dígitos, esta cantidad de números depende de quién crea la tarjeta).

En este caso los que eligen el dígito de control y el módulo son los fabricantes, que suelen ser por ejemplo MasterCard, Visa, American Express, Discover, JCB, Maestro, etc (nota sobre las marcas citadas: únicamente aparecen aquí algunas marcas como ejemplo para el aprendizaje y por aplicar el ejemplo en un contexto real).

Por estandarización suelen aplicar todos el “algoritmo de Luhn” que utiliza el módulo 10 (curiosidad sobre el módulo 10: siempre va a ser la última cifra del número, por ejemplo, para “576 mod 10” la última cifra de “576” es “6”).

¿Y el número que aparece detrás de la tarjeta bancaria (junto a la banda magnética)?

Ese número se conoce como “Código de Seguridad” (“Card Security Code” o “CSC”) o “CVV” o código “CVC”. Es un número de seguridad para asegurar que quién utilice la tarjeta (sobre todo por Internet, si has hecho alguna compra piden este número las pasarelas de pago) la posee físicamente. No confundir el “Código de Seguridad” con el “Dígito de control”. El “Código de Seguridad” por seguridad este código no puede ser almacenado en ningún sitio.

Por cumplir con la seguridad, tanto si tienes una página web -como si eres desarrollador- nunca, repito nunca, se almacenan los “Códigos de seguridad” de nadie en ningún sitio (como en una base de datos). Los “Códigos de seguridad” solo pueden estar almacenados en la tarjeta física, y el usuario lo tiene que introducir siempre que introduzca el “Número de la tarjeta” (salvo que la pasarela propia del banco que expidió la tarjeta haga lo contrario, pues ellos ya saben cuál es el “Código de Seguridad”, lo han creado ellos).

Repasamos los números de la tarjeta para dejarlos claros:

Por la cara de delante: El “Número de la tarjeta” que incluye al “Dígito de control”
Por la cara de atrás: El “Código de Seguridad”

Vamos a hacer de banco (o empresa) que expide la tarjeta a un cliente que la necesita de 16 dígitos (crearemos la tarjeta de la imagen anterior). Sabemos que el último número es el “Dígito de Control” por lo que podremos crear aleatoriamente (sin repetir con otros clientes) los 15 dígitos restantes, y para este ejemplo serán: “4455 8866 0022 445X” (“X” es el “Dígito de Control que tenemos que calcular con el “algoritmo de Luhn””)

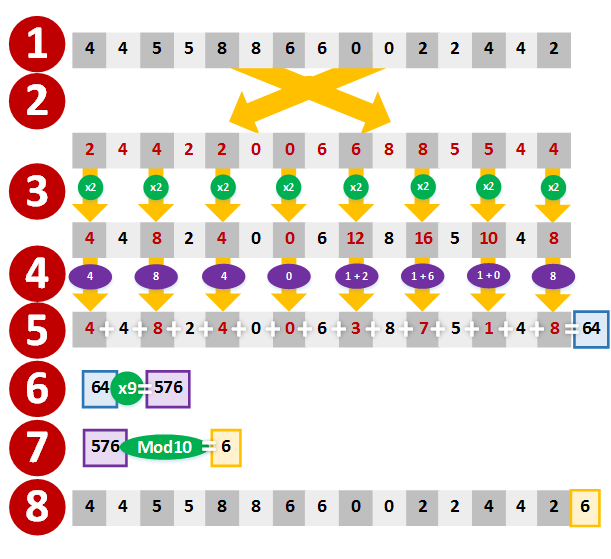
El “algoritmo de Luhn” es un algoritmo muy sencillo que puedes calcular a mano en menos de un minuto (palabra, lo he calculado a mano varias veces para hacer este ejemplo 😉 ). Los pasos son los siguientes (ve siguiendo la imagen con cada punto):

Teniendo ya el “Número de la tarjeta” menos el último número que será el “Dígito de Control”, y que hemos dicho que iba a ser “4455 8866 0022 445”; empezamos a calcular.
Invertimos los números (esto puede parecer poco importante, pero dependiendo de la cantidad de dígitos del “Número de la tarjeta” que como hemos dicho puede variar normalmente entre 12 y 19; así cumple siempre).
Multiplicamos por 2 (“x2”) los dígitos que ocupen las posiciones impares
Sumamos el dígito que representa las decenas más el que representa a las unidades de los resultados anteriores. Esto es, si en el paso 3 multiplicamos “8 x 2”, cuyo resultado es “16”; como se puede ver este resultado tiene varios dígitos (evidentemente cualquier número superior a “9” tiene varios dígitos), los sumamos “1 + 6” dando como resultado “7”. Sin embargo, si solo tiene un dígito, como puede ser “4” no hay que sumarlo a nada.
Sumamos todos los resultados anteriores.
Al resultado anterior lo multiplicamos por “9” (“x9”)
Realizamos el módulo 10 del resultado del paso previo. Cuyo resultado es finalmente el “Dígito de control”
Ya tenemos por completo el “Número de la tarjeta”, al poner al final de los números elegidos (recuerdo que eran “4455 8866 0022 445X”; sin invertir) el “Dígito de control” ahora calculado (tenemos “X” que es “6”, por lo que nos queda “4455 8866 0022 4456”). Ya se puede mandar a imprimir la tarjeta de crédito con un “Número de la tarjeta” válido 😉

Si por ejemplo queremos pagar con esta tarjeta en una página web, introduciríamos los 16 dígitos del “Número de la tarjeta” a mano, y puede que cometamos el error de introducir alguno de manera errónea o no. La pasarela de pago de la web calculará en el mismo navegador del usuario, mediante el “Algoritmo de Luhn”, si lo ha introducido bien o no, para indicar al momento al usuario si es correcto o no. Por lo que realizando otra vez el mismo “Algoritmo de Luhn” anterior, pero esta vez con el número introducido por el usuario a mano en la pasarela de pago de la web. Como ya se hizo en los pasos del algoritmo, no utilizamos el “Dígito de control” que ha introducido el usuario, sino que lo calculamos otra vez (como si volviéramos a expedir la tarjeta). Pues si coincide el “Dígito de control” ahora calculado con el que ha introducido el usuario, entonces el “Número de la tarjeta” será válido (por lo que el usuario habrá introducido el “Número de la tarjeta” correctamente); sino coincide con el “Dígito de control” introducido por el usuario, será que el usuario se ha equivocado en algún número, por lo que el “Número de la tarjeta” será invalido.

Documento Nacional de Identidad (DNI)

Aunque voy a poner de ejemplo el Documento de Identidad español, es parecido en otros documentos de otros países (Pista: en la página web oficial de cada gobierno o de quién lo expide, debería de venir información al respecto de los cálculos).

Para calcular el dígito de control del DNIe español (la imagen corresponde con el DNI antiguo, pero no cambia el cálculo para el ejemplo) podemos ver abajo a la izquierda el número donde pone “DNI NÚM.”, siendo el número “99999999” (normalmente el número del DNI es un número aleatorio, se entiende que este número es de ejemplo y no pertenece a ningún ciudadano) y el dígito de control es una letra asociada a un número, en este caso “R”.

Supongamos que somos los fabricantes de la tarjeta del DNI (En España la fábrica se llama “Casa de la moneda y timbre”), y queremos expedir/fabricar el DNI cuyo número es “99999999”. En el caso del DNI español el módulo es 23 (porque así lo ha decidido el gobierno). Entonces para calcular el dígito de control:

99999999 mod 23 = 1

Con lo que dígito de control es “1”. Ahora miramos en la tabla de mapeo entre números y letras (obtenida de http://www.interior.gob.es/web/servicios-al-ciudadano/dni/calculo-del-digito-de-control-del-nif-nie).

Y vemos que a “1” le corresponde efectivamente la letra “R”.

Para detectar un error podemos modificar uno o varios números, como por ejemplo “91995949-R”. Salvo colisiones (ver artículo de código Hash para más información sobre colisiones de códigos Hash), al hacer el cálculo anterior cambiará la letra:

91995949 mod 23 = 20

Cuya letra correspondiente a 20 es “C” que es diferente a la “R” puesta como dígito de control, por lo que ese número de DNI está mal.

Bibliografía

1 thoughts on “Dígito de control – Detección de errores”

sdfsfsdfsd dice:

31/10/2018 a las 17:33

heyt, muy bueno el de las tarjetas acabo de calar con una Visa de Debito que poseo para poner enpractica tu ejemplo aqui en Mexico que son de 16 caracteres y funciono.

Esto es algo que que ni sabia jajajaja muchas gracias

Responder

Deja una respuesta Cancelar la respuesta

Este sitio usa Akismet para reducir el spam. Aprende cómo se procesan los datos de tus comentarios.