Unidades de medida de la información
Es muy importante conocer las unidades de medida de la información, además de diferenciar entre el sistema antiguo y el nuevo (y la mezcla de ambos). Hay que tener una constancia mínima primero para que no nos “engañen” (¿El proveedor de Internet te está vendiendo realmente la velocidad de descarga que crees que estás pagando? ¿El disco duro o tarjeta de memoria que compraste tiene menos capacidad de la que creías antes de comprarlo?); y segundo, para poder trabajar con fluidez con ordenadores, tablets, smartphones, y demás aparatos digitales (¿Cuánto ocupa una foto o una película? ¿Aproximadamente cuánto va a tardar en descargarse un archivo o un juego? ¿Una aplicación está consumiendo muchos o pocos recursos de tu dispositivo?).
Conocemos muchos medios donde se guarda la información (Como discos duros o memorias RAM) y también donde se procesa (Como en procesadores). Para trabajar con esta información tenemos que conocer no solo como se utiliza sino como se mide.
“1 bit” puede ser un “0 binario” o bien un “1 binario”. El bit es la unidad de medida más pequeña de información, y que 1 no significa siempre 1 y 0 no significa casi nunca 0 (recomiendo leer este otro artículo sobre el bit, para aclarar dudas y entender el concepto de estados binarios). Igual que cualquier otra unidad de medida, como los “litros” que se utilizan para medir el volumen (muy utilizado para líquidos, como la cantidad de agua o lo que ocupa el zumo de fruta), los “gramos” para medir el peso, o los “metros” para medir la distancia; pero con el bit medimos la cantidad de información (sería como contar las letras de un libro, pero a mucho menor nivel como veremos).
Pensamos en «1 bit» es una caja vacía que puede tener algo o no (el 1 o el 0 binario), y ese “algo” o el “vacío” representa información (puedes imaginar que tengo un amigo que sabe que si introduzco cualquier cosa dentro de la caja significa “compra pasteles”, y si dejo la caja vacía quiere decir “compra fruta”; le estoy transmitiendo información a mi amigo, y él sabe qué hacer con esa información, aunque nadie más conozca el significado de esta caja, o incluso para otra persona puede que tuviera otra interpretación sobre si la caja tiene algo o no).
Imagina que eres dueño de una empresa de memorias RAM (o de discos duros o de tarjetas de memoria, lo que quieras, pues es semejante; para el ejemplo voy a usar memorias RAM porque se ve muy bien en los dibujos la idea).
Nota sobre el ejemplo:
Para este ejemplo voy a representar las memorias RAM con forma de tarjeta (se utilizan en ordenadores de sobremesa y portátiles; los smartphones y tablets llevan los chips de memoria RAM directamente integrados en la placa base), cada una de estas tarjetas se llama “módulo de memoria RAM”.
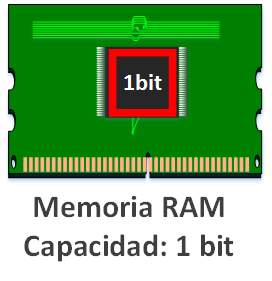
Como estamos empezando con nuestra empresa, nuestra primera memoria RAM solo tendrá 1 bit de capacidad (en la que solo cabe un “0 binario” o un “1 binario”, uno de los dos estados).
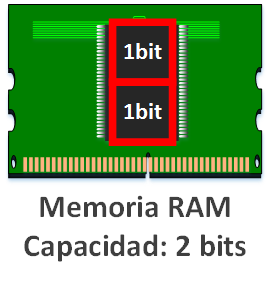
Vivimos en una época en la que los ordenadores están naciendo, con lo que no tenemos competencia y todos nos compran nosotros nuestra maravillosa memoria RAM de 1 bit, pero rápidamente surge la competencia y hay que mejorar nuestro producto. Cómo eres el fabricante quieres ganar dinero, así que tienes que pensar en obtener el máximo beneficio al mínimo coste (es decir, comprar materiales baratos y que la fabricación sea barata, para vender a los clientes el producto resultante al máximo precio posible que estén dispuestos a pagar). Con estas premisas, lo mejor es utilizar el menor material posible que tenga la máxima calidad viable al precio que queramos construir cada módulo de memoria RAM. Nos interesa duplicar la capacidad del chip central de nuestra memoria RAM para que quepa más información. Con ello tenemos nuestra tarjeta de memoria de 2 bits.
Además, los usuarios desearán que la memoria que fabriquemos ocupe el mínimo espacio posible y tenga la máxima capacidad. Así que tenemos que indicar cuánto espacio queremos que ocupe (por ejemplo, el tamaño de un disco duro o de un módulo de memoria RAM). Entonces para que ocupe el mínimo espacio y empleando los mínimos recursos lo más sencillo es aprovechar al máximo los materiales (del chip los cables internos, el plástico, el silicio, etc …) para fabricar más bits.
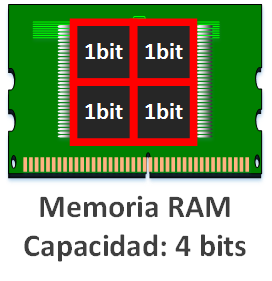
Añadir un 1 bit más -para que haya 3 bits en la memoria RAM- sale muy caro, pues colocarlos en forma triangular desaprovechamos los recursos. Lo más óptimo para el precio de gastar en materiales y la capacidad es ya saltar directamente a 4 bits.
Además -como fabricante- cuando queramos vender un “dispositivo de almacenamiento de datos” (“dispositivo de almacenamiento de datos” suele ser un disco duro, un DVD, o un módulo de memoria RAM, por ejemplo) al consumidor, venderemos el doble de la tecnología anterior (que es lo que suele verse en las tiendas con los productos digitales, como los nuevos discos duros de 1 TiB, después de 2 TiB, al poco de 4 TiB, luego de 8 TiB, etc).
Ampliación del artículo de «Bit»:
Si has leído el artículo que recomendé de sobre los estados de un Bit, ahí tratamos con la tecnología de núcleos magnéticos (que está muy bien para tener una visión general sobre cómo se escriben y leen los bits). Si no, puedes saltarte este cuadro.
En este artículo he mostrado el módulo de “memoria RAM” actual que bien podrías estar basado en la tecnología SRAM (Static Random Access Memory, o en español “memoria estática de acceso aleatorio”; basada en semiconductores) o en la tecnología DRAM (Dynamic Random Access Memory, o en español “memoria dinámica de acceso aleatorio”; basada en condensadores). Pero también existía la memoria de núcleos magnéticos (conocida como “memoria de toros” que explicamos en el anterior artículo, puedes ver más información en https://es.wikipedia.org/wiki/Memoria_de_toros ) que era similar a la memoria RAM. Pero la idea de fabricación es la misma:
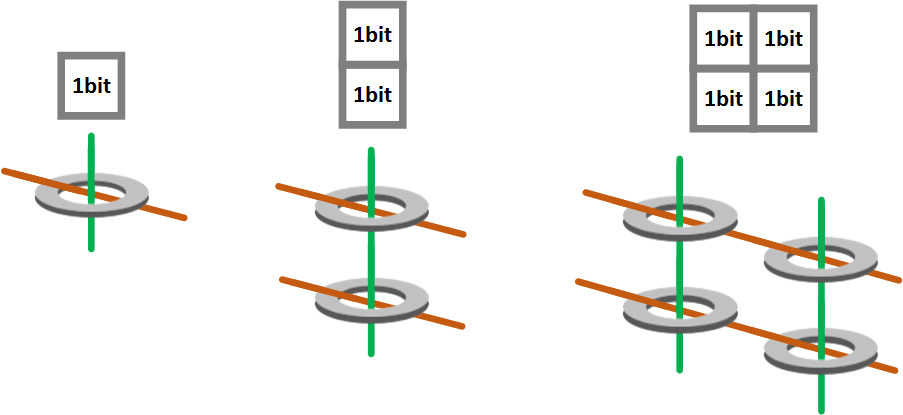
- 1 núcleo magnético es capaz de guardar 1 bit
- 2 núcleos magnéticos, aprovechando uno de los cables, es capaz de guardar 2 bits
- 4 núcleos magnéticos, aprovechando dos de los cables, es capaz de guardar 4 bits
- etc.
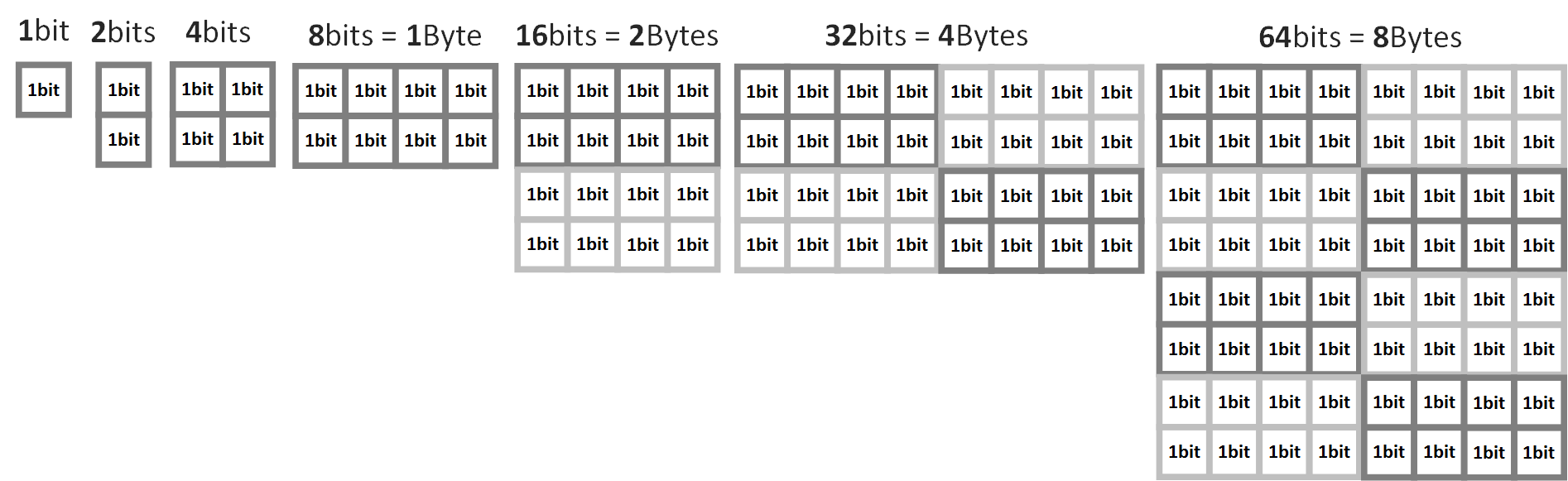
En la anterior imagen represento encima la capacidad en cuadrados de 1 bit cada cuadrado (a una memoria de 1 núcleo magnético le cabe 1 bit, a una de 2 núcleos magnéticos le caben 2 bits, a una de 4 le caben 4 bits).
Aprovechando los cables para que sea óptimo, resulta que siempre conseguimos potencias de dos cada vez que ampliamos.
A partir de aquí voy a representar los bits en cuadrados pues no tienen por qué ser “memorias RAM” o “núcleos magnéticos” (más arriba tienes ejemplo de “memorias RAM” y de “núcleos magnéticos” con los bits ocupando cuadrados).
Dicho así, si empezamos con 1 bit (recomiendo que acompañes este párrafo con la siguiente imagen de izquierda a derecha; la palabra “Byte” la explico a continuación y los tonos de gris de los cuadrados son agrupaciones de 8 bits para que quede más visual), el doble de lo anterior serán 2 bits (2 x 1 bit), el doble de lo anterior 4 bits (2 x 2 bits), el doble de lo anterior 8 bits (2 x 4 bits), el doble de lo anterior 16 bits (2 x 8 bits), el doble de lo anterior 32 bits (2 x 16 bits), el doble de lo anterior 64 bits (2 x 32 bits), y así hasta el infinito.
Como puedes ver esto crece muy deprisa, por lo que ya tenemos que buscar un nombre que agrupe varios bits para que nos facilite trabajar con ellos. Por ejemplo ¿Sería sencillo que tu amigo entendiera si le decimos que “grabe en su ordenador una película que ocupa 858.993.459.200 bits” porque está en calidad 4K? Creo que así de primeras nuestro amigo sabría que “858.993.459.200 bits” es mucho, sin calculadora no podría asegurar si cabe en la memoria de su ordenador; pero si le dices a tu amigo que ocupa 100Gib la cosa cambia, es más fácil para tu amigo conocer rápidamente si va a caber la película en su ordenador o no).
Razones por las que las memorias se fabrican en potencias de dos:
Indicar que también existen otras razones por la que las memorias vienen en potencias de dos, como:
- Como se indicó, fabricar las memorias en potencias de dos ahorra costes.
- Es más fácil trabajar con potencias de dos al ser números binarios (al igual que, seguramente, te es muy sencillo trabajar en potencias de 10 con números decimales ¿Cuál de las dos siguientes operaciones te es más fácil multiplicar de cabeza: “79.584×9.879” o “79.584×10.000”?)
- Por la optimización del direccionamiento de memoria (por ejemplo, si tenemos varios módulos de memoria RAM, para la CPU es más rápido leer datos de los distintos módulos de memoria RAM en potencias de dos, pues no tiene que hacer muchos cálculos)
Por el tamaño fijo de las palabras en bytes (la cantidad de bits mínimos con los que siempre trabaja el procesador o las memorias; aunque solo queramos procesar 5 bits puede que el mínimo a procesar sean 32 bits, por lo que se procesarán los 32 bits que incluyen nuestros 5 bits, pero solo nos importan esos 5 bits y los 27 bits restantes se descartarán; veremos estos más adelante)
Byte
Por ello, la unidad de medida después del bit es el byte, que es una agrupación de 8 bits (1 byte = 8 bits). Echa un vistazo a la anterior imagen otra vez, he pintado en diferentes tonos de gris los grupos de 8 bits (lo que representa 1 byte) para que se vean de inmediato.
¿Y por qué 8 bits y no un número redondo como él 10? Por la razón que hemos explicado antes de “fabricar el doble de lo que había anteriormente”. Es más fácil para los fabricantes crear espacios de más tamaño duplicando lo que ya había anteriormente. Lo que en matemáticas se conoce como potencias de dos (dos elevado a algún número, se representa como 2n ), es decir, un dos multiplicado así mismo un número de veces:
- 1 = 20
- 2 = 21
- 4 = 2×2 = 22
- 8 = 2x2x2 = 23
- 16 =2x2x2x2 = 24
- 32 = 2x2x2x2x2 = 25
- 64 = 2x2x2x2x2x2 = 26
- 128 = 2x2x2x2x2x2x2 = 27
- 256 = 2x2x2x2x2x2x2x2 = 28
- 512 = 2x2x2x2x2x2x2x2x2 = 29
- 1024 = 2x2x2x2x2x2x2x2x2x2 = 210
- Y así hasta el infinito …
De los anteriores números seguro que algunos reconoces inmediatamente como “digitales”. Cuando en los anuncios comerciales o en el propio envoltorio del producto ponen cosas como (no te centres en las siglas, pues pueden ser raras y confusas, simplemente lee los ejemplos de anuncios y te explicaré luego):
- “Portátil con disco duro SSD de 512 GiB y 16 GiB de memoria RAM”
- “Tarjeta de memoria SD para cámaras de 128 GiB de capacidad”
- “Nuevo disco duro de 16 TiB”
- “Procesador con memoria caché L1 de 32 KiB, L2 de 256 KiB y L3 de 8 MiB”
¿“GiB”, no se dice sin la “i” GB? Aunque se pueden decir de las dos maneras, tenemos que atender a la nueva nomenclatura, que indica cantidades diferentes de bits. Por ejemplo, no es la misma cantidad de bits 4GB que 4GiB. Existe mucha confusión y quiero que quede muy claro para siempre, ahora lo descubrirás.
Lo primero y más importante, es tener muy claro que 1 bit es la unidad básica y 1 byte son 8 bits. Más importante es como se representan. El símbolo (la palabra acortada a una o unas pocas letras) para bit es una “b” (minúscula) y para byte es una “B” (mayúscula). De este modo, puedes decir que tienes una memoria de “16b” o lo que es lo mismo de “2B” (2B = 2 x 8b = 16b). De este párrafo lo que podría resultar en confusión es que “b” pequeña (minúscula) es lo más pequeño, que es 1 bit; y “B” grande (mayúscula) son varios bits, en concreto un grupo de 8 bits. Estas “letras bes” (“b” y “B”) se ponen de sufijo (al final) de otros prefijos multiplicadores (como la G de “Giga”: Gb o GB).
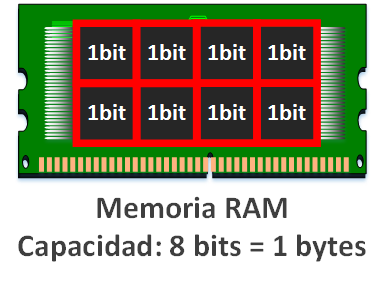
Volviendo al ejemplo de ser fabricantes de módulo de “memorias RAM”. Para la siguiente tecnología ya tendríamos 1 byte (1B = 8b) de capacidad.
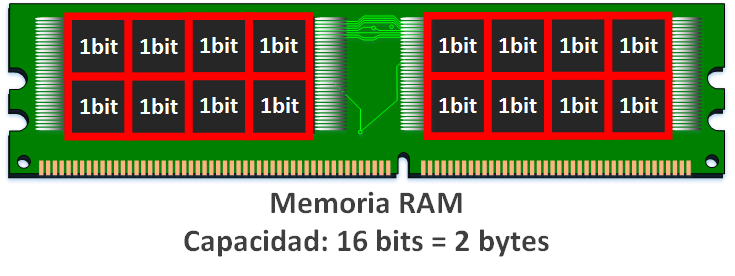
Existe cierto momento en el que ya no nos interesa crecer más lo que es el chip de la memoria (porque se caliente demasiado, porque es más barato duplicar el chip, porque ocupa menos si ponemos varios o por otros motivos) sino que es mejor poner varios chips de memoria del mismo tamaño. En nuestro ejemplo nos interesa poner varios chips de memoria para duplicar la capacidad total del módulo de memoria RAM. Así tendremos una memoria RAM de 16 bits (lo que son 2 bytes) de capacidad.
Unidades de medida
Pero no nos podemos quedar solo en 8 bits, existen representaciones mucho mayores que en combinación con las anteriores nos sirven para representar el tamaño de la información (los tamaños de las memorias).
Nota sobre la puntuación en los números decimales de este artículo: A continuación, utilizo la representación del punto como separador de miles (ejemplo: 1.000.000) y la coma como separador de decimales (ejemplo: 1.000.000,37).
De prefijo se ponen algunos conocidos como la “k”, que seguro lo has visto en varios sitios como con el dinero (en el ejemplo utilizo el símbolo monetario del Euro al final, sustitúyelo por el que te sea cómodo): “Hemos ganado 25k €” que quiere decir que “Hemos ganado 25.000 €” (o lo que es lo mismo que 25 mil euros). Por lo que la “k” significa “mil” o “kilo”, y por tanto para medir la información (en informática) también 1k = 1.000 bits, lo que es 10 elevado a 3 (reprentado como 103 , así que: 1k = 10x10x10 = 103 = 1.000 ).
¡Espera un segundo! ¿No hemos quedado que trabajamos con potencias de dos (2 elevado a algo, 2n )? He visto muchas veces k de kilo referido en términos de informática como potencia de 2, concretamente 2 elevado a 10 que es igual a 1.024 ( 210 = 1.024 ), y no a 1.000 ( 103 = 1.000 ) ¿Qué es lo que está mal?
Sí y por desgracia lo seguirás viendo mal escrito (esperemos que por poco tiempo). Fue un error humano que se está corrigiendo con el tiempo, y, mientras, no nos queda otra más que convivir con el error.
Realmente no fue un error “aposta” sino de falta de representación. Antaño (por el 1964) cuando se empezaron a inventar los ordenadores, no existía una nomenclatura para trabajar con los bits y se utilizaba la que había, como por ejemplo la k de kilo. Pero -como hemos visto- la memoria siempre se crea en potencias de dos.
Piensa en una época en la que fabricamos la primera memoria de 1.024 bits. Queremos representar esta cantidad un poco más “redonda y bonita” (pues 1.024 bits son 128 Bytes, y ya hablar de 128 se nos hace un número “grande y feo”). Sabemos que en todo el mundo el “kilo” representa “1.000”, que se acerca mucho al número “1.024”, por lo que es muy sencillo para la gente utilizar las siglas que ya conoce (y no tener que inventarnos palabras que no existían). Así que, decidimos resumir 1024 bits y llamarlos 1 kilobit ¡Perfecto! Acabamos de cometer el “error” que nos trae hoy día de cabeza. Resulta que se estuvo utilizando la palabra kilo para multiplicar todo lo que te puedas imaginar por 1000, salvo para los bits que se multiplicarían por 1024 (y no en todos los casos).
Este error se extendió para toda la tabla de múltiplos enteros del sistema internacional de unidades (más información del sistema internacional de unidades en https://es.wikipedia.org/wiki/Sistema_Internacional_de_Unidades ), desde entonces se utilizaron mal todos los prefijos para múltiplos decimales enteros (“múltiplos decimales” son potencias de 10, es decir, lo que queramos medir por 10 elevado a algo; y “enteros” porque no tenía sentido decir la “mitad de 1 bit” si el 1 bit era la unidad más pequeña): kilo, mega, giga, peta, exa, zetta, yotta, etc
Por bastantes años estuvieron conviviendo representaciones como (para este artículo interesa solo que te enteres de «bits» y «bytes», pero que entiendas el contexto de la implicación):
- 16 km = 16.000 metros (16 x 1.000)
- 16 kg = 16.000 gramos (16 x 1.000)
- 16 ks = 16.000 segundos (16 x 1.000)
- 16 kA = 16.000 amperios (16 x 1.000)
- 16 kK = 16.000 kelvines (16 x 1.000)
- 16 kmol = 16.000 moles (16 x 1.000)
- 16 kcd = 16.000 candelas (16 x 1.000)
- 16 kcal = 16.000 calorías (16 x 1.000)
- 16 kW = 16.000 Vatios (16 x 1.000)
- 16 kV = 16.000 Voltios (16 x 1.000)
- 16 kb = 16.384 bits (16 x 1.024)
- 16 kB = 16.384 Bytes (16 x 1.024)
Vamos que era y es un lío, hay que pensar en potencias de 10 para la mayoría de las cosas y potencias de 2 solo los bits (facilitaba caer en errores de cálculo; se terminaba asociando mentalmente kilo a 1024, lo mismo con mega y giga, luego venían los errores). Te terminabas acostumbrando, pero no dejaba de ser complejo y poco práctico; sobre todo para lo que realmente sirven estas representaciones unificadas y estandarizadas, para entendernos y comunicarnos de una forma efectiva entre todos los que somos en el planeta Tierra.
Así que se propuso un nuevo sistema de representación para las potencias de dos (se respetó las potencias de diez, pues ya existían de antes; le tocó cambiar a la representación que vino después, por mucho que le pese a los bits). Y es muy sencillo, principalmente se basa en introducir una “i” (i latina minúscula) al final del prefijo (por ejemplo, kib o kiB para las potencias de 2; dejando kb o kB para las potencias de 10). Con ello conseguimos una clara diferencia entre decimal y binario. Esta “i” viene de “binary”, el prefijo completo es “bi”. Así “kilo” quedaba reservado para 10 elevado a 3 y “kibi” para 2 elevado a 10. Por fin corregimos y podemos decir las cosas con propiedad, dependiendo de la cantidad de bits que queramos expresar:
- 16 kilobits = 16 kb = 16.000 bits (16 x 1.000)
- 16 kilobytes = 16 kB = 16.000 Bytes (16 x 1.000) = 128.000 bits (8 x 16 x 1.000)
- 16 kibibits = 16 kib = 16.384 bits (16 x 1.024)
- 16 kibibytes = 16 kiB = 16.384 Bytes (16 x 1.024) = 131.072 bits (8 x 16 x 1.024)
Como curiosidad, lo mismo nos sirve para otras unidades de medida. Podría pedir al frutero que me ponga 3 kig (3 kibigramos = 3 x 1024 = 3072 gramos) de manzanas que es más que 3kg (3 kilogramos = 3 x 1000 = 3000 gramos) de manzanas, aunque puede que el frutero me mirase extrañado 😛
Indicar que esta nueva unidad en potencias de 2 fue definida por la Comisión Electrotécnica Internacional (más de IEC en https://es.wikipedia.org/wiki/Comisi%C3%B3n_Electrot%C3%A9cnica_Internacional)
Además de las unidades antes citadas, si has utilizado o comprado algún smartphone, Tablet, portátil, cámara digital, ordenador, etc (si estás leyendo este artículo supondré que con bastante probabilidad has escuchado las siguiente unidades cientos de veces). Seguro que te has topado con la multiplicación en potencias de 10 en bastantes características de los productos. Por ejemplo:
- Procesador de 3,2 Ghz (Gigaherzio) = procesador cuya frecuencia es de 3.200.000.000 hercios (3,2 x 1.000.000.000)
- Cámara de fotos de 12 Mpx (Megapixel) = La cámara es capaz de capturar 12.000.000.000 pixeles (12 x 1.000.000.000) por foto
Confusiones con algunas unidades:
- Televisión con 4K = pantalla que tiene cerca de 4000 pixeles en la horizontal (la “K” mayúscula de 4K aunque quiere expresar los 1000 no significa 1000, para eso tendría que ser 4k con “k” en minúscula. “4K” es el nombre de una tecnología). 4K hay de varios formatos como Full 4K (resolución de 4096 pixeles de ancho × 2160 pixeles de alto) o 4K UHDV (de 3840 x 2160)
- Batería de 3.000 mAh = 3 Amperios durante una hora (la “m” es minúscula significa “mili” y equivale a «10 elevado a -3», 10-3 = 0,001; “mAh” son “miliamperios hora”, por lo que 3000 x 0,001 = 3 Ah)
Nota sobre lo que puede implicar el cambio de unidades para lo que lo hemos aprendido de la manera antigua: Al escritor de este artículo le duele más que los que estáis empezando a estudiar esto, pues yo lo tuve que aprender con el “error” y ahora me toca hacer el doble esfuerzo para decir las cosas bien. Si estás empezando, entonces te toca convivir con los dos símbolos. Es interesante conocer lo que estaban mal para que no te “engañen”, y aplicar el que está bien hasta que algún día solo se utilice el que está bien (hay que utilizar cada unidad de medida tal y como se estandarizó).
Tablas de múltiplos
Hay que tener muy clara la diferencia entre los múltiplos que representa cada prefijo de los estándares actuales:
Comisión Eléctrica Internacional (ISO/IEC 80000)
En potencias de 2 (el que principalmente nos interesa por facilidad de realizar cálculos binarios y por lo explicado anteriormente). Se caracteriza por incluir “bi” (de binario) en el texto de la unidad de medida, o la “i” en el símbolo.
| Prefijo | Símbolo | Cantidad de bits (en decimal) |
| kibi- | ki | 210 = 1.024 |
| mebi- | Mi | 220 = 1.048.576 |
| gibi- | Gi | 230 = 1.073.741.824 |
| tebi- | Ti | 240 = 1.099.511.627.776 |
| pebi- | Pi | 250 = 1.125.899.906.842.624 |
| exbi- | Ei | 260 = 1.152.921.504.606.846.976 |
| zebi- | Zi | 270 = 1.180.591.620.717.411.303.424 |
| yobi- | Yi | 280 = 1.208.925.819.614.629.174.706.176 |
Sistema Internacional de Unidades (SI)
En potencias de 10.
| Prefijo | Símbolo | Cantidad de bits (en decimal) |
| kilo- | k | 103 = 1.000 |
| mega- | M | 106 = 1.000.000 |
| giga- | G | 109 = 1.000.000.000 |
| tera- | T | 1012 = 1.000.000.000.000 |
| peta- | P | 1015 = 1.000.000.000.000.000 |
| exa- | E | 1018 = 1.000.000.000.000.000.000 |
| zetta- | Z | 1021 = 1.000.000.000.000.000.000.000 |
| yotta- | Y | 1024 = 1.000.000.000.000.000.000.000.000 |
Nota sobre el símbolo «k»:
el símbolo “k” de “kilo-” es en minúscula, y la “k” de “ki” de “kibi-” también es en minúscula (no confundir pues el símbolo “K” mayúscula que representa la unidad Kelvin, y sirve para medir temperatura). Salvo la “k”, el resto de símbolos se escriben en mayúsculas.
Ya sabemos lo que representa cada símbolo. Ahora tenemos que poner a cada prefijo el sufijo que nos interese de bit o byte que hemos visto anteriormente.
Tabla de múltiplos básicos de bit y byte
Fácil, ya la sabemos:
| Unidad de medida | Símbolo | Cantidad de bits (en decimal) |
| 1 bit | b | 20 = 1 bit |
| 1 byte | B | 23 = 8 bits |
Antes de mostrarte las tablas completas con los bits o bytes, quiero enseñarte lo sencillo que es escribir y entender estos símbolos (es tan sencillo como multiplicar todo: el número y los símbolos divididos, salvo el de unidad que es indivisible; veamos ejemplos). Por ejemplo ¿Qué significa “37 Mib”?
- 37 es la cantidad que multiplica que vienen detrás “Mib”
- Hay que separar los símbolos “Mi” y “b”
- “Mi” sabemos que es 220 que es igual a 1.048.576
- “b” es la unidad indivisible, que podemos decir que vale 1 (decimal) la unidad, pero queremos que signifique su palabra “bit”
- Multiplicamos todos los números: 37 x 1.048.576 = 38.797.312 (utilizamos una calculadora para calcular el resultado). Entonces “37 Mib” es igual a “38.797.312 bits” (hemos añadido la palabra “bit” que representa la unidad al final, para saber que estamos hablando de “bits” y no de otra cosa; pues si le digo a mi amigo “tengo 38.797.312”, él me va a preguntar seguro “¿Tienes 38.797.312 qué cosas?”)
He incidido en la “unidad” puesta al final por dos razones: una para entendernos y otra por la siguiente razón ¿Qué significa “37 MiB”? Hagamos lo mismo que antes:
- 37 x MiB
- “MiB” consta de “Mi” y “B”
- Mi = 220 = 1.048.576
- ¡Ojo! Tenemos que entender el significado de “B”, que significa “byte”, y 1 byte son 8 bits. 1byte = 8 bits (o con símbolos: 1 B = 8 b)
- Aquí tenemos dos opciones, dependiendo de cómo queramos dejar el resultado, si en bytes o en bits (para este último nos toca multiplicar por 8 para pasar de 1 byte a 8 bits):
a. 37 x 1.048.576 = 38.797.312 bytes
b. 37 x 1.048.576 x 8 = 310.378.496 bits
¡Esto de dividir y multiplicar los símbolos es un peñazo!
Te puedo prometer que se aprende muy rápido (es todo igual multiplicando por unas cosas o por otras). Si le dedicas un poco de tiempo te aseguro que te será tan sencillo como el sumar y tan útil que no querrás dejar de utilizarlo 🙂
Esto no solo se aplica a las unidades binarias. También a cosas más mundanas y físicas (que puedes sujetar y utilizar a tu alrededor), como por ejemplo ¿Qué significa que en una caja tengamos “37 Kg” en lingotes de oro puro?
- 37 x kg
- “kg” consta de “k” y “g”
- k = 103 = 1.000
- 37 x 1.000 = 37.000 g de oro puro
- Pero no lleguemos hasta aquí, profundicemos hasta la unidad básica de cualquier cosa “el átomo” (para este ejemplo “un átomo” sería el equivalente a “un bit” binario para las cosas físicas; el átomo se divide en más cosas, pero aquí me vale con entender el átomo como se creía antiguamente “Sin división”, para ponerlo en equivalencia con el “bit” en el ejemplo). Nota sobre química: No tienes que saber química para entender este artículo, aquí pongo un ejemplo gratuito para entender la relación entre las unidades abstractas y físicas, que si cabe son más fáciles las unidades binarias que las unidades de lo “físico y mundano”, y que los cálculos son iguales cambiando de valores; sino lo entiendes o no tienes ganas de leer química básica, puedes saltarte este cuadro (por otro lado, si sigues leyendo te llevas una clase gratuita de química básica 🙂 )
- Sabemos que 1 mol de cualquier cosa son 6,022 × 1023 átomos (número de Avogadro redondeado, https://es.wikipedia.org/wiki/Mol). Nota de ejemplo: el “mol” que es un grupo de átomos (concretamente 1 mol son 602.214.129.000.000.000.000.000 átomos), sería el equivalente binario al “byte” que es un grupo de “bits” (concretamente 1 byte son 8 bits)
- Sabemos que 1 mol de oro pesa 196,967 g (masa atómica del oro redondeada, que podemos consultar en la tabla periódica de los elementos químicos; para el oro hay más información en https://es.wikipedia.org/wiki/Oro)
- Entonces 37.000 gramos dividido entre 196,967 gramos (el peso de 1 mol de oro), obtendríamos la cantidad de moles. 37.000 / 196,967 = 187,85 moles de oro
- Ya solo nos queda multiplicar los moles por la cantidad de átomos que tiene cada mol (1 mol = 6,022 × 1023 átomos). 187,85 x 6,022 × 1023 = 1.131.232.700.000.00.000.000.000.000 átomos hay en 37 kg de oro
Va a resultar que son más fáciles de calcular las unidades de «información» que «las químicas» 😀
En favor a cualquier sistema de unidades. Si entiendes uno y sabes usarlo, el resto es igual cambiando los valores (es decir, son todos igual de sencillos, aunque luego tengas que entender para que sirve cada uno).
Las siguientes tablas se escriben solas al saber interpretar y formar los símbolos de multiplicación de unidades anteriores. Pero siempre es bueno tener estas tablas a mano para ir rápidamente al resultado, y aquí te las quiero dejar.
Mantengo los colores de las tablas en naranja para la “Comisión Eléctrica Internacional” y en azul para el “Sistema Internacional de Unidades”.
Comisión Eléctrica Internacional (ISO/IEC 80000) para bits
| Unidad de medida | Símbolo | Cantidad de bits (en decimal) |
| 1 kibibit | kib | 210 = 1.024 bits |
| 1 mebibit | Mib | 220 = 1.048.576 bits |
| 1 gibibit | Gib | 230 = 1.073.741.824 bits |
| 1 tebibit | Tib | 240 = 1.099.511.627.776 bits |
| 1 pebibit | Pib | 250 = 1.125.899.906.842.624 bits |
| 1 exbibit | Eib | 260 = 1.152.921.504.606.846.976 bits |
| 1 zebibit | Zib | 270 = 1.180.591.620.717.411.303.424 bits |
| 1 yobibit | Yib | 280 = 1.208.925.819.614.629.174.706.176 bits |
Comisión Eléctrica Internacional (ISO/IEC 80000) para bytes
| Unidad de medida | Símbolo | Cantidad de bits (en decimal) |
| 1 kibibyte | kiB | 8 x 210 = 8.192 bits |
| 1 mebibyte | MiB | 8 x 220 = 8.388.608 bits |
| 1 gibibyte | GiB | 8 x 230 = 8.589.934.592 bits |
| 1 tebibyte | TiB | 8 x 240 = 8.796.093.022.208 bits |
| 1 pebibyte | PiB | 8 x 250 = 9.007.199.254.740.992 bits |
| 1 exbibyte | EiB | 8 x 260 = 9.223.372.036.854.775.808 bits |
| 1 zebibyte | ZiB | 8 x 270 = 9.444.732.965.739.290.427.392 bits |
| 1 yobibyte | YiB | 8 x 280 = 9.671.406.556.917.033.397.649.408 bits |
Sistema Internacional de Unidades (SI) para bits
| Unidad de medida | Símbolo | Cantidad de bits (en decimal) |
| 1 kilobit | kb | 103 = 1.000 bits |
| 1 megabit | Mb | 106 = 1.000.000 bits |
| 1 gigabit | Gb | 109 = 1.000.000.000 bits |
| 1 terabit | Tb | 1012 = 1.000.000.000.000 bits |
| 1 petabit | Pb | 1015 = 1.000.000.000.000.000 bits |
| 1 exabit | Eb | 1018 = 1.000.000.000.000.000.000 bits |
| 1 zettabit | Zb | 1021 = 1.000.000.000.000.000.000.000 bits |
| 1 yottabit | Yb | 1024 = 1.000.000.000.000.000.000.000.000 bits |
Sistema Internacional de Unidades (SI) para bytes
| Unidad de medida | Símbolo | Cantidad de bits (en decimal) |
| 1 kilobyte | kB | 8 x 103 = 8.000 bits |
| 1 megabyte | MB | 8 x 106 = 8.000.000 bits |
| 1 gigabyte | GB | 8 x 109 = 8.000.000.000 bits |
| 1 terabyte | TB | 8 x 1012 = 8.000.000.000.000 bits |
| 1 petabyte | PB | 8 x 1015 = 8.000.000.000.000.000 bits |
| 1 exabyte | EB | 8 x 1018 = 8.000.000.000.000.000.000 bits |
| 1 zettabyte | ZB | 8 x 1021 = 8.000.000.000.000.000.000.000 bits |
| 1 yottabyte | YB | 8 x 1024 = 8.000.000.000.000.000.000.000.000 bits |
Hemos de tener clara la diferencia para los tipos de medidas de tamaño binario, así evitar confundirnos:
- Sin prefijo. Ejemplo: 1B = 1 byte
- Prefijos binarios con símbolos de la Comisión Electrotécnica Internacional (IEC). Ejemplo: 1kiB = 1.024 bytes
- Prefijos binarios con símbolos del Sistema Internacional (SI). Ejemplo: 1kB = 1.024 bytes (La antigua y “errónea” forma de representar el tamaño binario)
- Prefijos decimales con símbolos del Sistema Internacional (SI). Ejemplo: 1kB = 1.000 bytes
Con esto ya no nos engañarán más y sabremos quién todavía utiliza la manera antigua (la errónea).
Calculadoras Online
También podemos ayudarnos de calculadoras para realizar las conversiones.
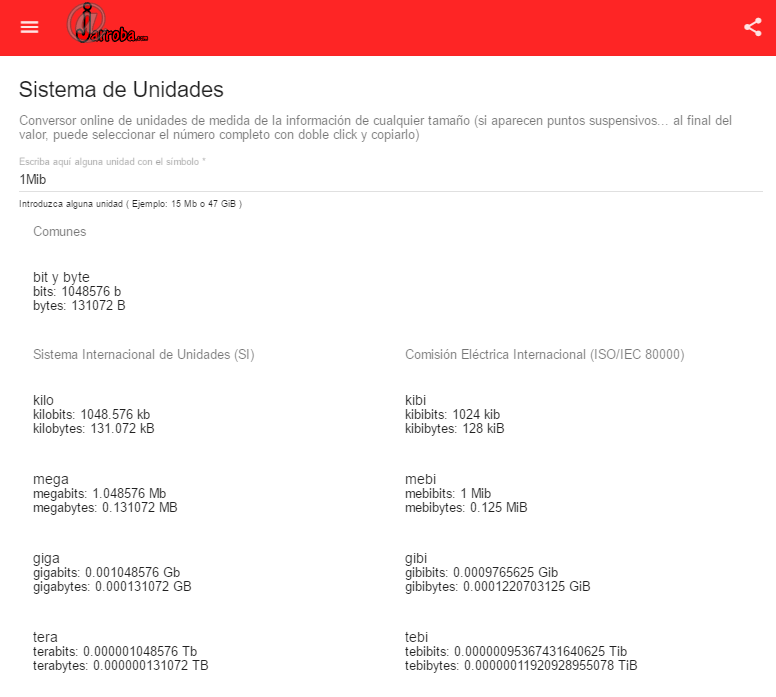
Como la Calculadora Online de Jarroba para convertir cualquier valor automáticamente a todos los demás. Solo hay que introducir un valor y la calculadora te sugiere automáticamente los valores (Puedes comprobar el resultado directamente en la siguiente dirección https://jarroba.com/tools/unitsystem/1Mib ). Una característica muy importante y útil es que puedes probar con cualquier valor da igual el tamaño, pues no tiene límite de entrada ni de salida, calcula números enormes y a todos los valores a la vez (y puedes compartir el resultado).
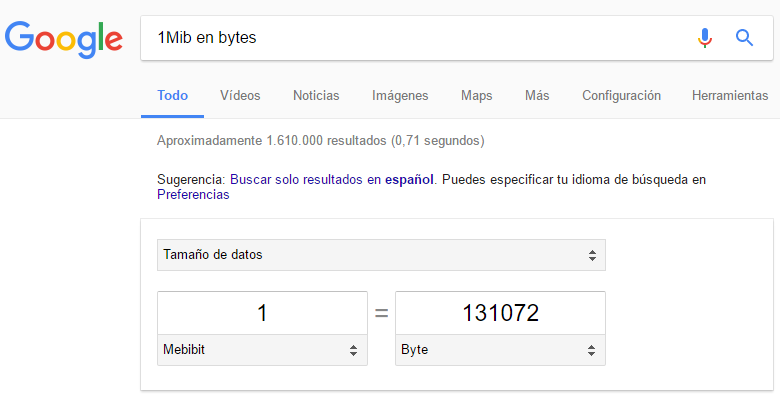
O como la Calculadora online de Google. Es suficiente con buscar lo que quiero convertir en el buscador de Google, como por ejemplo “1Mib en bytes” (El resultado de la búsqueda del ejemplo la puedes comprobar en la siguiente dirección: https://www.google.es/webhp?sourceid=chrome-instant&ion=1&espv=2&ie=UTF-8#q=1Mib+en+bytes&* )
Confusiones más típicas de la unidades
Ejemplos de confusión en productos
Unos párrafos más arriba te he engañado, y no sé si te has dado cuenta, pero ¡qué más da! el hecho es que te he engañado a propósito en como los fabricantes y anuncios promocionan sus productos. De los anteriores “anuncios de material tecnológico” más bien lo que se suele ver es:
- “Portátil con disco duro SSD de 512 GB y 16 GB de memoria RAM”
- “Tarjeta de memoria SD para cámaras de 128 GB de capacidad”
- “Nuevo disco duro de 16 TB”
- “Procesador con memoria caché L1 de 32 KB, L2 de 256 KB y L3 de 8 MB”
¡Ups! Ya no está tan claro que quieren decir los anunciantes y fabricantes ¿Cuándo hablan por ejemplo de “GB” se refieren realmente a “GB” como potencias de 10? o ¿Están usando erróneamente “GB” como forma antigua cuando quieren decir “GiB” (potencias de 2, 2n )? Esta diferencia es importante, pues no es lo mismo que se refieran a 512 GB como 512 GiB que 512 GB del Sistema Internacional de unidades, pues:
- 512 GB = 512 x 109 x 8 = 4.096.000.000.000 bits
- 512 GiB = 512 x 230 x 8 = 4.398.046.511.104 bits
Lo más común es que creamos que nos están vendiendo un disco duro de 512 GiB, y si realmente estamos comprando uno de 512 GB estamos perdiendo:
4.398.046.511.104 bits – 4.096.000.000.000 bits = 302.046.511.104 bits
Que son en GiB (dividimos en vez de multiplicar para convertir de bits a GiB):
302.046.511.104 bits = 302046511104 / 230 / 8 = 35,17 GiB
¡Nos están vendiendo de menos 35,17 GiB (donde caben 7200 fotos de 5MiB cada una, o 7 películas de DVD estándar de 4,7GiB) respecto a lo que queríamos!
Y cuánto más grande sea, con este problema de entendimiento más estamos perdiendo respecto a lo que realmente pensábamos. Por eso, cuando compramos algún medio de almacenamiento parece que ha perdido espacio con el simple hecho de enchufarlo ¡No ha perdido espacio, nos están confundiendo con las unidades que no es lo mismo! (algunas veces está justificada la pérdida de espacio al comprar un producto, por ejemplo, si compramos un portátil con el sistema operativo instalado, si el disco duro era de 512 GiB y el sistema operativo ocupa cerca de 50 GiB pues es esto de menos que tenemos; pero cuando compramos de vacío no tanto y para esto hay que tener cuidado.
El truco para ver que nos están vendiendo realmente es mirar la etiqueta o pedir que nos digan el espacio en bytes o en bits. Si ves que en la caja del producto pone en grande 512 GB, si lo miramos en bytes tiene que ser cercano a 512.000.000.000 bytes (512 GB del Sistema Internacional) o a 549.755.813.888 bytes (512 GiB); no voy a decirte que no se pierde nada del producto (el caso de un disco duro o tarjeta de memoria vacía hay ciertos datos de arranque del propio producto que ocupan espacio del mismo producto), pero a alguna de estas dos cifras se acerca seguro.
Y si aun así no está claro lo que te quieren vender (recomiendo preguntar para salir de dudas). Pienso que es mejor asumir por norma estándar (el nuevo) que, por ejemplo, “512 GB” son 512.000.000.000 bytes y no 549.755.813.888 bytes (512 GiB) por dos razones:
- Si leo GB en un producto (las unidades en potencias de 10) ¿Por qué no nos vamos a fiar si es el estándar universal? Ya pondrían GiB si quieren decir GiB y no GB
- GB siempre va a ser menor que GiB (las potencias de 10 son menores que la de 2, por ejemplo, 1kb son 1000 bits mientras que 1kib son 1024 bits). Así me aseguro que al menos no me timen, y si luego me llevo la sorpresa de que es más pues mejor.
Es importante estar atentos para evitar confusiones y que no nos “engañen” algunos vendedores o fabricantes, que a sabiendas de la confusión (que nos vendan GB como GB del Sistema Internacional que es bastante menos que el GiB), o simplemente por no confundir a viejos consumidores con sus productos (para ellos el GB significa GiB). Si en el producto ya viene las nuevas unidades (que venga como GiB) pues perfecto, no hay confusión ninguna; pero sino, hay que calcular un poco para evitar trampas (no hay que olvidar que es legal el hecho de “engañar” o aprovechar el desconocimiento o la verdad parcial sobre la confusión de representación de las unidades digitales).
Ejemplo de confusión en publicidad de servicios (Conexión a Internet)
Este es un ejemplo publicitario real, muy recurrente, que aprovecha de la máxima confusión de los sistemas de unidades.
Un ejemplo de máxima confusión en los anuncios suele ser en las telecomunicaciones, cuando nos venden una conexión a Internet:
- “Nueva oferta de conexión a Internet de 300 Mbps de bajada y 100 Mbps de subida”
¿Mbps? Significa “Megabits por segundo”, es lo máximo que te va a ofrecer tu operador (es decir, no significa que vayas a descargar a 300 Mb por segundo; si tienes suerte, debido a varios factores como la distancia a la central o problemas en la red, como máximo alcanzarás 300 Mb por segundo de descarga) ¿Y cómo mínimo que ofrece la operadora? Depende del contrato, puede ser un porcentaje mínimo que te aseguren o no haya mínimo (si hay mínimo, por ejemplo, el 20% de lo contratado, como mínimo serían 240 Mbps de 300 Mbps; sino hay mínimo, podría ser 0 Mbps)
¿No está en Bytes? No. Tendrían que poner el anuncio con una velocidad aparente “8 veces” inferior (la conversión de 8 bits a 1 byte), y les interesa que aparente 8 veces más (estrategia de Marketing, decir la verdad pero que aparente lo que queremos que aparente). Por ejemplo: 300 Mb / 8 = 37,5 MB por segundo
¿Y la “M” de “mega” en qué sistema está expresado? En el Sistema Internacional de unidades, es decir en potencias de 10 (que es menor al “mebi” en potencias de dos que vimos antes)
Entonces ¿Cuánto son 300 Mb en MiB? Calculemos, primero convirtiendo a una unidad común a los dos sistemas de unidades y luego transformándolo a la nueva (si no quieres hacer cálculos, puedes utilizar las calculadoras online que te enseñé antes):
300 Mb = 300 x 106 = 300.000.000 bits = 300.000.000 / 220 / 8 = 35,76 MiB
Vamos, que de los grandiosos 300 Mb por segundo de máximo que nos ofrecían las operadoras de Internet en los anuncios, la velocidad expresada correctamente en bytes no aparenta ser tan buena, pues es solo de 35,76 MiB por segundo (pero es solo una ilusión tanto que 300 Mb parece mucho, como 35,76 MiB que parece poco; en términos lógicos y reales 300 Mb = 35,76 MiB ¡Que no nos engañen las apariencias!).
La mayoría de usuarios caen en el truco de pensar que “Mbps” son “MiB por segundo”, y como te he mostrado no es así.
Nota sobre los test de velocidad que hay por Internet: Al menos todos lo que he encontrado y he utilizado están expresados en Mbps (Megas del Sistema Internacional y en bits). No he encontrado ninguno que lo exprese en bytes o en «mebi», para que veas hasta donde llega el “truco” publicitario y que como usuario no te sea sencillo averiguar la “trampa”. Aunque siempre tienes el derecho a saber la verdad y aquí te la hemos demostrado 😀
Ejemplo de confusión en información en pantalla
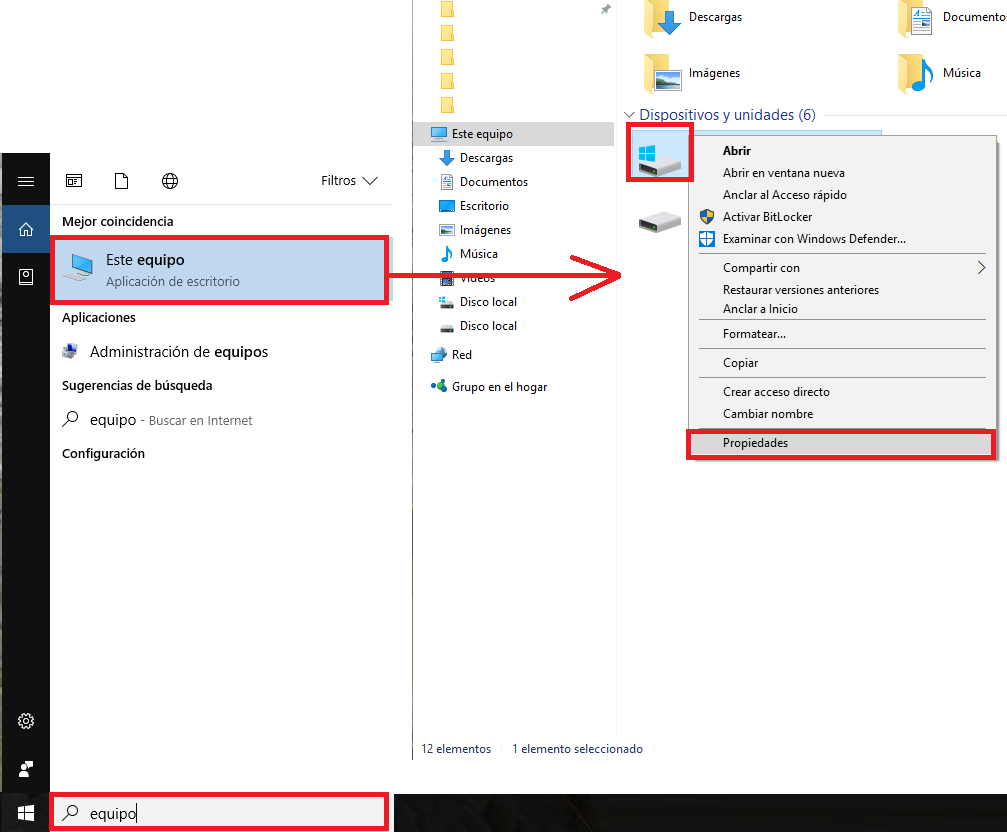
Otro ejemplo bastante común. Si eres usuario Windows y consultas el espacio de disco duro (Escribir “Equipo” en el cuadro de abajo a la izquierda de la barra de tareas Windows; con el botón derecho del ratón elegir un disco duro de tu ordenador; luego pulsar “Propiedades”)
¡Resulta que las unidades vienen expresadas de la forma antigua 🙁 ! Aparecen GB, MB, etc.
Aunque soy partidario de utilizar el nuevo sistema de unidades, en este caso voy a justificar a Windows (pues una empresa que se dedica a desarrollar Software y Hardware no creo que se le escapen estas cosas). Resulta que un conjunto muy grande de la población sigue utilizando las viejas y erróneas conversiones, no todos se arriesgan a cambiar de GB a GiB para no confundir a sus usuarios (aunque sea lo correcto cambiarlo). Podemos perdonarles pues también añaden los bytes, con lo que podemos calcular lo que queramos. Si haces la conversión de la imagen de arriba de cualquier unidad de bytes a GiB, por ejemplo, veamos el de 931GB:
1.000.068.870.144 bytes = 1.000.068.870.144 / 230 = 931,37 GiB
De aquí el truco. Para que todo sea comprensible, lo mejor es que convirtamos de bytes o bits a la unidad que queramos, así no hay confusión alguna.
En un futuro, es previsible que Windows cambie de sistema de representación de unidades.
Por otro lado, otros sistemas operativos como Ubuntu, sí que utilizan correctamente las unidades. Por ejemplo, cuando aparecen GB son en el sistema internacional, o bien como GiB y la respectiva conversión de valores.
Referencias
- https://en.wikipedia.org/wiki/Units_of_information
- https://en.wikipedia.org/wiki/ISO/IEC_80000
- https://en.wikipedia.org/wiki/Metric_prefix
- https://es.wikipedia.org/wiki/Comisi%C3%B3n_Electrot%C3%A9cnica_Internacional
- https://en.wikipedia.org/wiki/Binary_prefix
- https://es.wikipedia.org/wiki/Resoluci%C3%B3n_4K



Mal fundamentado tu titulo seria unidades de medida del dato mas no de la informacion.