Expectation-maximization en Python y Scikit-learn, con ejemplos
- El proyecto de este post lo puedes descargar pulsando AQUI.
- Este post forma parte del libro "Machine Learning (en Python), con ejemplos"
El Expectation-maximization (EM) es un método estadístico de Clustering similar al K-means, pero con un enfoque probabilístico. Este método asume que todos los objetos (del data set) han sido generados a partir de ‘k’ distribuciones de probabilidad de las cuales desconocemos a priori sus parámetros.
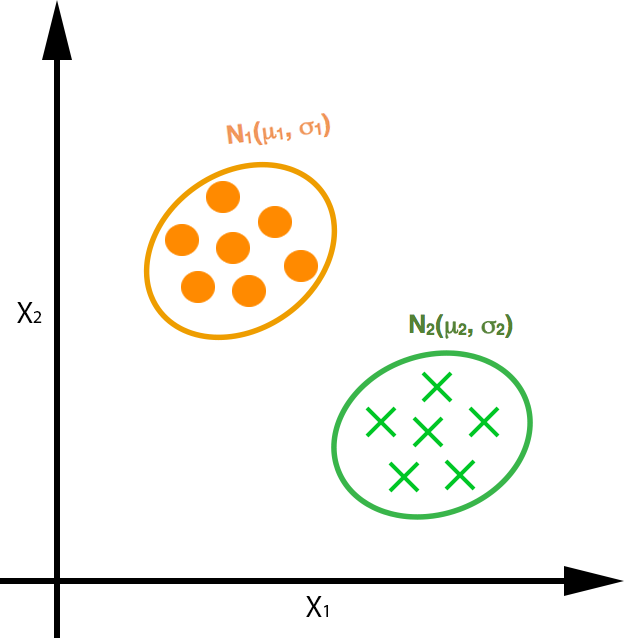
Para entender que queremos resolver con el EM, supongamos el siguiente caso en el que sabemos que dos grupos de objetos (Clusters) se generan de acuerdo a dos distribuciones normales (gaussianas) p(x|μ,σ) definidas por su media (μ) y su desviación típica (σ):
En este ejemplo conocemos los parámetros de las distribuciones normales (la media y desviación típica) y por tanto; dado un punto cualquiera, vamos a saber a que Cluster pertenece o a que distribución de probabilidad pertenece (o tiene más probabilidades de pertenecer).
Planteemos ahora el problema al revés, en el que tenemos un conjunto de objetos de los cuales desconocemos los parámetros de las distribuciones de probabilidad que los generan (en el caso de una distribución normal su media y desviación típica); o dicho de otra manera, el data set no nos aporta la información suficiente para saber como han sido creados los modelos probabilísticos asumidos. Esta falta de información (o información ausente) en los datos de entrenamiento se denomina “datos perdidos” o “variables latentes”.
El EM tiene por tanto como finalidad el encontrar; a partir de los datos de entrenamiento (data set), los parámetros de las distribuciones de probabilidad que asumimos que han generado estos datos; o dicho de una manera un poco más formal, encontrar estimadores de máxima verosimilitud de los parámetros de los modelos estadísticos que dependen de las variables latentes.
Aunque el EM es un método que puede ser aplicado sobre cualquier distribución de probabilidad (no tiene porque ser solo sobre distribuciones normales debido a que no sabemos la naturaleza de los datos de los que disponemos), vamos a pasar a continuación a explicar en detalle los cálculos y pasos a dar para calcular los parámetros de ‘k’ distribuciones normales, asumiendo que los objetos de nuestro data set se han generado de acuerdo a ‘k’ distribuciones normales p(x|μ,σ); por tanto, podemos agrupar estos datos en ‘k’ Clusters.
A igual que el K-means, debemos de definir previamente cuantos Clusters vamos a tener para agrupar los objetos. Supongamos que elegimos 3 Clusters (K=3). Dado un objeto de nuestro data set, asumimos que este sigue una de las tres distribuciones normales; por tanto, tendrá una determinada probabilidad ‘π’ de pertenecer a cada uno de los Clusters. A priori decimos, que tendrá un 33.3% de pertenecer al Cluster 1, un 33.3 % de pertenecer al Cluster 2 y un 33.4% de pertenecer al Cluster 3. Una vez que tengamos más conocimiento de los objetos que hay en cada Cluster, esta probabilidad por Cluster cambiará; por ejemplo, si tenemos 100 objetos de los cuales 50 están en el Cluster 1, 35 están en el Cluster 2 y 15 están en el Cluster 3; decimos que dado un punto, este tendrá un 50% de pertenecer al Cluster 1, un 35% de pertenecer al Cluster 2 y un 15% de pertenecer al Cluster 3.
Por otro lado; para cada una de las distribuciones de probabilidad, tenemos que calcular sus parámetros; y en este caso asumiendo que se siguen distribuciones normales, debemos de calcular la media y la desviación típica de cada una de ellas en función de los objetos de data set. Una vez vayamos ajustando estos valores; según se va ejecutando el algoritmo del EM, cada uno de los objetos del data set tendrá una probabilidad determinada de pertenecer a cada unos de los Clusters; por tanto (y de forma similar al K-means con las distancias), cada objeto pertenecerá a aquel Cluster cuya probabilidad sea mayor (el producto de πi · pi(x|μ,σ)).
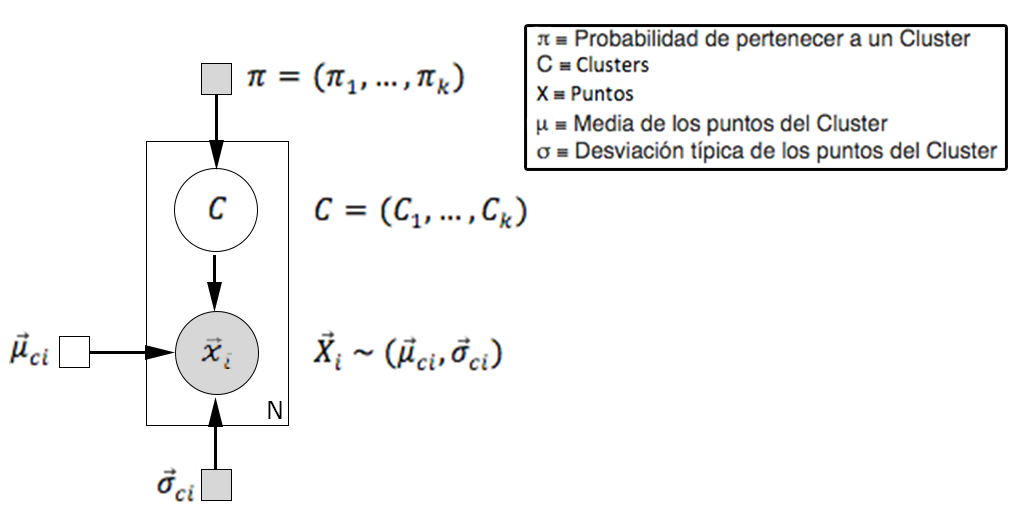
A continuación se muestra en representación “Plate Notation” el EM para distribuciones normales (gaussianas):
En la imagen anterior definimos los círculos como distribuciones de probabilidad y los cuadrados como escalares o vectores, siendo los de fondo gris valores o distribuciones de probabilidad conocidas y las de fondo blanco desconocidas; y que por tanto hay que calcular. Lo que viene a representar la imagen anterior es que tenemos ‘N’ objetos en el que cada unos de ello ‘xi’ esta en una distribución de probabilidad con media ‘μi’ desconocida (y que por tanto hay que calcular) y desviación típica ‘σi’ conocida. Cada uno de los objetos puede pertenecer con una probabilidad ‘πi’ a cada uno de los ‘k’ Clusters ‘C’, asignando finalmente un objeto concreto del data set al Cluster cuya probabilidad definida como el producto de ‘πi’ por pi(x|μi,σi) sea la mayor de todas.
El problema a resolver es por tanto el calcular la probabilidad de pertenencia de un objeto a cada uno de los Cluster. Para ello tenemos lo siguiente:
Lo que nos interesa saber es la probabilidad de pertenencia de un objeto a cada uno de los Clusters:
Tenemos por otro lado que P(C│π) es un valor constante (P(c=1│π1 ), P(c=2│π2 ), …, P(c=k│π_k )), cosa que nos ayuda a la hora de realizar el cálculo de probabilidades quedando de la siguiente manera:
Aplicando la función de densidad de una distribución normal, tenemos que la suma de todas las probabilidades de pertenencia de un punto a los Clusters es:
Podemos simplificar esta probabilidad ya que 1/√2π es una constante, quedando:
Esto último lo podemos hacer ya que lo que nos interesa es asignar el objeto al Cluster con mayor probabilidad; es decir:
Una vez definido el cálculo de la probabilidad de pertenencia de un objeto a un Cluster, vamos a explicar el funcionamiento del EM, que como se podrá apreciar va a tener un comportamiento muy similar al K-means, teniendo dos pasos: el paso de esperanza (expectation) y el paso de maximización (maximization) que es similar a los pasos de asignación y actualización del K-means respectivamente.
El funcionamiento del EM comienza inicializando los parámetros de las distribuciones de probabilidad y probabilidades de pertenencia a los Clusters. Esto lo podemos hacer de muchas manera, proponiendo por ejemplo inicializar la probabilidad de pertenencia a un Cluster ‘π’ como 1/k y para las distribuciones normales inicializar con desviación típica a ‘1’ y la media inicializándola con el valor de un punto del data set. Una vez inicializados los parámetros, el algoritmo continua alternando los dos siguientes pasos (esperanza y maximización) de forma iterativa hasta que las medias de las distribuciones normales converjan:
- Esperanza (Expectation): Con los parámetros conocidos de las distribuciones normales y la probabilidad ‘π’ de pertenencia a un Cluster, asignar cada objeto al Cluster con el mayor valor de probabilidad de pertenencia:
- Maximización (Maximization): Calcular con los objetos asignados a cada Cluster el valor de los parámetros (πk, μk y σk):
Definido el funcionamiento del algoritmo paso por paso, pasamos a mostrarlo en pseudocódigo:
En los dos siguientes puntos: Implementación del Expectation-maximization y Expectation-maximization (Gaussian mixture models) con scikit-learn, se va a mostrar la implementación del EM asumiendo que los datos son generados en base a distribuciones normales y el uso de la librería scikit-learn para la resolución de un problema de Clustering con el algoritmo del Gaussian mixture models (mezcla de modelos gaussianos) respectivamente, cuyo código se puede obtener en el siguiente repositorio:
https://github.com/RicardoMoya/ExpectationMaximization_Python
El código que se encuentra en este repositorio hace uso de las librerías de numpy, matplotlib, scipy y scikit-learn. Para descargar e instalar (o actualizar a la última versión con la opción -U) estas librerías; con el sistema de gestión de paquetes pip, se deben ejecutar los siguiente comandos:
pip install -U numpy pip install -U matplotlib pip install -U scipy pip install -U scikit-learn
Implementación del Expectation-maximization
En este apartado se va a mostrar la implementación del EM (desde un punto de vista didáctico) en el que los objetos van a estar representados por un punto en dos dimensiones {x,y}. La implementación realizada en este ejemplo permite que los objetos puedan estar representados con más dimensiones, pero sin perder la perspectiva didáctica de este ejemplo los mostramos en dos dimensiones para que podamos visualizar los resultado en un plano y así entender el correcto funcionamiento de este método.
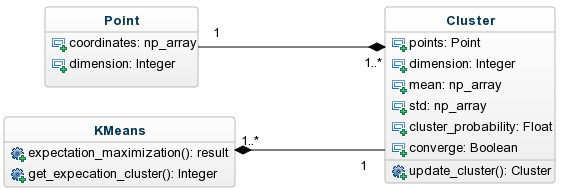
Para implementar el EM, vamos a tener objetos que serán representados como puntos en 2D, por tanto implementaremos una clase Punto (Point.py) para representar los objetos. Por otro lado se implementa una clase Cluster (Cluster.py) para representar a los Clusters y que estará compuesta por un conjunto de objetos de la clase Punto. Por último tendremos un script (EM.py) en el que estará implementado del EM para distribuciones normales con sus dos pasos de esperanza y maximización para ‘k’ Clusters. A continuación se muestra a un alto nivel de abstracción el diagrama de clases de la implementación propuesta del EM:
Los data sets a utilizar en este ejemplo (que se encuentran dentro de la carpeta dataSet) van a ser ficheros de texto en los que en cada línea van a estar las coordenadas de cada punto {x,y} separados por el separador “::”. A continuación mostramos un ejemplo de estos ficheros:
1.857611652::2.114033851 2.34822574::1.58264984 1.998326848::4.118143019 1.714362835::2.468639613 1.656134484::1.909955747
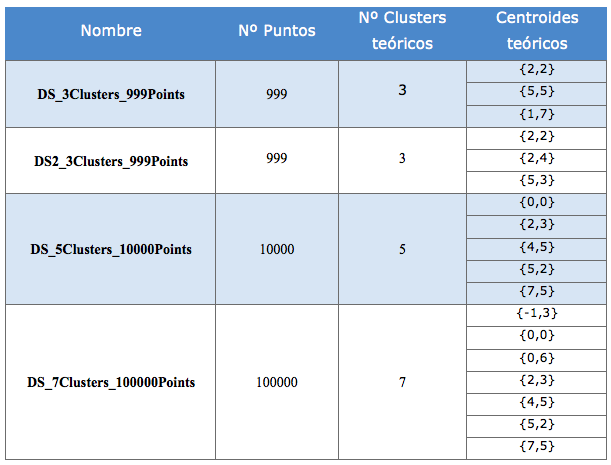
Esto quiere decir que el primer punto va a estar posicionado en las coordenadas {1.85,2.11} y el segundo punto en las coordenadas {2.34,1.58}.
Para los ejemplos disponemos de 4 data sets con las siguientes características:
Visto el diagrama de clases y la estructura de los date sets a utilizar, vamos a pasar a mostrar la implementación de la clases Punto (Point.py). A esta clase se le va a pasar en el constructor un “numpy array” con las coordenadas del punto y va a tener como atributos esa coordenada y las dimensiones de la misma, que para el ejemplo que vamos a mostrar será de 2:
class Point:
def __init__(self, coordinates):
self.coordinates = coordinates
self.dimension = len(coordinates)
def __repr__(self):
return 'Coordinates: ' + str(self.coordinates) + \
'\n\t -> Dimension: ' + str(self.dimension)
Por otro lado vamos a tener la clase Cluster (Cluster.py) que se le va a pasar en el constructor una lista de puntos que van a ser los que formen el Cluster y el número de elementos del Cluster que lo forman. Esta clase va a tener como atributos la lista de puntos del Cluster (points), la dimensión de los puntos (dimension), la media de los puntos del Cluster (mean), la desviación típica de los puntos del Cluster (std), la probabilidad ‘’ de pertenencia al Cluster (cluster_probability) y un atributo (converge) que nos va a indicar si la media es igual (por tanto converge) que el calculado en el paso de maximización de la iteración anterior. Veamos a continuación el constructor de esta clase:
import numpy as np
class Cluster:
def __init__(self, points, total_points):
if len(points) == 0:
raise Exception("Cluster cannot have 0 Points")
else:
self.points = points
self.dimension = points[0].dimension
# Check that all elements of the cluster have the same dimension
for p in points:
if p.dimension != self.dimension:
raise Exception(
"Point %s has dimension %d different with %d from the rest "
"of points") % (p, len(p), self.dimension)
# Calculate mean, std and probability
points_coordinates = [p.coordinates for p in self.points]
self.mean = np.mean(points_coordinates, axis=0)
self.std = np.array([1.0, 1.0])
self.cluster_probability = len(self.points) / float(total_points)
self.converge = False
Por otro lado implementamos el método update_cluster(points), que es el método encargado de actualizar los parámetros del modelo probabilístico que define el Cluster, calculando la media y la desviación típica de la distribución normal y la probabilidad ‘’ de pertenencia al Cluster; en definitiva, este método realiza el paso de maximización. Este método también comprueba si convergen las medias de la distribución de una iteración a otra. En resumen, con este método actualizamos los parámetros del modelo probabilístico que define al Cluster.
def update_cluster(self, points, total_points):
old_mean = self.mean
self.points = points
points_coordinates = [p.coordinates for p in self.points]
self.mean = np.mean(points_coordinates, axis=0)
self.std = np.std(points_coordinates, axis=0, ddof=1)
self.cluster_probability = len(points) / float(total_points)
self.converge = np.array_equal(old_mean, self.mean)
Una vez explicadas las Clases Punto y Cluster que necesitamos para estructurar la información, vamos a pasar a explicar la implementación del EM propiamente dicha. Esta implementación esta en el script EM.py que mostramos a continuación y que posteriormente vamos a explicar cada fragmento de código relevante:
# -*- coding: utf-8 -*-
__author__ = 'RicardoMoya'
import random
import math
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from Point import Point
from Cluster import Cluster
DATASET1 = "./dataSet/DS_3Clusters_999Points.txt"
DATASET2 = "./dataSet/DS2_3Clusters_999Points.txt"
DATASET3 = "./dataSet/DS_5Clusters_10000Points.txt"
DATASET4 = "./dataSet/DS_7Clusters_100000Points.txt"
NUM_CLUSTERS = 3
ITERATIONS = 1000
COLORS = ['red', 'blue', 'green', 'yellow', 'gray', 'pink', 'violet', 'brown',
'cyan', 'magenta']
def dataset_to_list_points(dir_dataset):
"""
Read a txt file with a set of points and return a list of objects Point
:param dir_dataset: path file
"""
points = list()
with open(dir_dataset, 'rt') as reader:
for point in reader:
points.append(Point(np.asarray(map(float, point.split("::")))))
return points
def get_probability_cluster(point, cluster):
"""
Calculate the probability that the point belongs to the Cluster
:param point:
:param cluster:
:return: probability =
prob * SUM(e ^ (-1/2 * ((x(i) - mean)^2 / std(i)^2 )) / std(i))
"""
mean = cluster.mean
std = cluster.std
prob = 1.0
for i in range(point.dimension):
prob *= (math.exp(-0.5 * (
math.pow((point.coordinates[i] - mean[i]), 2) /
math.pow(std[i], 2))) / std[i])
return cluster.cluster_probability * prob
def get_expecation_cluster(clusters, point):
"""
Returns the Cluster that has the highest probability of belonging to it
:param clusters:
:param point:
:return: argmax (probability clusters)
"""
expectation = np.zeros(len(clusters))
for i, c in enumerate(clusters):
expectation[i] = get_probability_cluster(point, c)
return np.argmax(expectation)
def print_clusters_status(it_counter, clusters):
print '\nITERATION %d' % it_counter
for i, c in enumerate(clusters):
print '\tCluster %d: Probability = %s; Mean = %s; Std = %s;' % (
i + 1, str(c.cluster_probability), str(c.mean), str(c.std))
def print_results(clusters):
print '\n\nFINAL RESULT:'
for i, c in enumerate(clusters):
print '\tCluster %d' % (i + 1)
print '\t\tNumber Points in Cluster: %d' % len(c.points)
print '\t\tProbability: %s' % str(c.cluster_probability)
print '\t\tMean: %s' % str(c.mean)
print '\t\tStandard Desviation: %s' % str(c.std)
def plot_ellipse(center, points, alpha, color):
"""
Plot the Ellipse that defines the area of Cluster
:param center:
:param points: points of cluster
:param alpha:
:param color:
:return: Ellipse
"""
# Matrix Covariance
cov = np.cov(points, rowvar=False)
# eigenvalues and eigenvector of matrix covariance
eigenvalues, eigenvector = np.linalg.eigh(cov)
order = eigenvalues.argsort()[::-1]
eigenvector = eigenvector[:, order]
# Calculate Angle of ellipse
angle = np.degrees(np.arctan2(*eigenvector[:, 0][::-1]))
# Calculate with, height
width, height = 4 * np.sqrt(eigenvalues[order])
# Ellipse Object
ellipse = Ellipse(xy=center, width=width, height=height, angle=angle,
alpha=alpha, color=color)
ax = plt.gca()
ax.add_artist(ellipse)
return ellipse
def plot_results(clusters):
plt.plot()
for i, c in enumerate(clusters):
# plot points
x, y = zip(*[p.coordinates for p in c.points])
plt.plot(x, y, linestyle='None', color=COLORS[i], marker='.')
# plot centroids
plt.plot(c.mean[0], c.mean[1], 'o', color=COLORS[i],
markeredgecolor='k', markersize=10)
# plot area
plot_ellipse(c.mean, [p.coordinates for p in c.points], 0.2, COLORS[i])
plt.show()
def expectation_maximization(dataset, num_clusters, iterations):
# Read data set
points = dataset_to_list_points(dataset)
# Select N points random to initiacize the N Clusters
initial = random.sample(points, num_clusters)
# Create N initial Clusters
clusters = [Cluster([p], len(initial)) for p in initial]
# Inicialize list of lists to save the new points of cluster
new_points_cluster = [[] for i in range(num_clusters)]
converge = False
it_counter = 0
while (not converge) and (it_counter < iterations):
# Expectation Step
for p in points:
i_cluster = get_expecation_cluster(clusters, p)
new_points_cluster[i_cluster].append(p)
# Maximization Step
for i, c in enumerate(clusters):
c.update_cluster(new_points_cluster[i], len(points))
# Check that converge all Clusters
converge = [c.converge for c in clusters].count(False) == 0
# Increment counter and delete lists of clusters points
it_counter += 1
new_points_cluster = [[] for i in range(num_clusters)]
# Print clusters status
print_clusters_status(it_counter, clusters)
# Print final result
print_results(clusters)
# Plot Final results
plot_results(clusters)
if __name__ == '__main__':
expectation_maximization(DATASET1, NUM_CLUSTERS, ITERATIONS)
Lo primero que se hace al ejecutar el script es llamar el método expectation_maximization() al que se le pasa como parámetros el data set que contiene el conjunto de puntos, el número de Clusters que queremos obtener y el número máximo de iteraciones a realizar por si no convergen nunca las medias de las distribuciones de probabilidad. Estos parámetros los tenemos definidos como constantes en el script ya que tenemos disponibles 4 data sets.
if __name__ == '__main__':
expectation_maximization(DATASET1, NUM_CLUSTERS, ITERATIONS)
El método expectation_maximization() implementa el EM tal y como se indica en el pseudocódigo mostrado anteriormente. En primer lugar leemos de un fichero el data set con el método dataset_to_list_points(file) e inicializamos las ‘N’ distribuciones que definen los Clusters (num_clusteres) con la media seleccionando de forma aleatoria ‘N’ puntos del data set. Posteriormente iniciamos los pasos de esperanza y maximización hasta que estos converjan o hasta que lleguemos al número máximo de iteraciones (iterations). Esto lo hacemos dentro del bucle “While”. En cada iteración asignamos cada uno de los puntos del data set a la distribución de probabilidad que mayor probabilidad de pertenencia tenga (el producto de πi • pi(x|μi,σi)) con el método get_expectation_cluster() que devuelve el índice de la distribución (o el Cluster), y una vez asignados recalculamos los parámetros de las distribuciones de probabilidad. Posteriormente comprobamos la convergencia para ver si seguimos iterando o no. En la implementación vemos los métodos print_clusters_status(), print_results() y plot_results() que son métodos auxiliares que utilizamos para mostrar los parámetros de las distribuciones de probabilidad que definen los Clusters en cada iteración y mostrar y pintar (con la librería matplotlib) el resultado final:
def expectation_maximization(dataset, num_clusters, iterations):
points = dataset_to_list_points(dataset)
# INICIALIZACIÓN: Selección aleatoria de N puntos para inicializar la media de
# las de las distribuciones normales que definen un Cluster
initial = random.sample(points, num_clusters)
# Create N initial Clusters
clusters = [Cluster([p], len(initial)) for p in initial]
# Inicializamos una lista para el paso de esperanza (Expectation)
new_points_cluster = [[] for i in range(num_clusters)]
converge = False
it_counter = 0
while (not converge) and (it_counter < iterations):
# Esperanza
for p in points:
i_cluster = get_expecation_cluster(clusters, p)
new_points_cluster[i_cluster].append(p)
# Maximización
for i, c in enumerate(clusters):
c.update_cluster(new_points_cluster[i], len(points))
# ¿CONVERGE?
converge = [c.converge for c in clusters].count(False) == 0
# Incrementamos el contador
it_counter += 1
new_points_cluster = [[] for i in range(num_clusters)]
print_clusters_status(it_counter, clusters)
print_results(clusters)
plot_results(clusters)
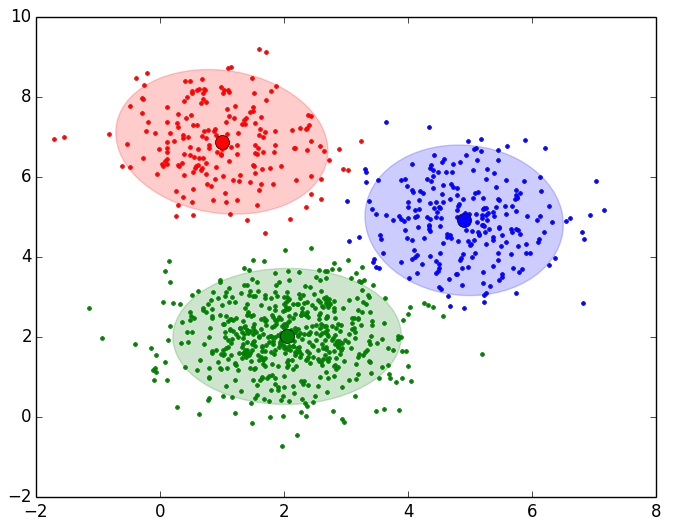
Veamos a continuación un ejemplo de la ejecución de este script en el que se mostrará el estado de cada Cluster en cada una de las iteraciones hasta la obtención del resultado final. Para el ejemplo utilizaremos el data set 1 (DATASET1) que tiene 999 y que los agruparemos en 3 Clusters:
1.- Elección de 3 puntos al azar para inicializar las medias de las distribuciones normales. Por otro las inicializamos la desviación típica a ‘1’ y la probabilidad de pertenencia a un Cluster como 1/3:
Cluster 1: Probability = 0.33; Mean = [ 1.77 6.21]; Std = [ 1. 1.]; Cluster 2: Probability = 0.33; Mean = [ 4.97 6.91]; Std = [ 1. 1.]; Cluster 3: Probability = 0.33; Mean = [ 2.39 1.49]; Std = [ 1. 1.];
2.- Iniciamos las iteraciones: Iteración 1
Cluster 1: Probability = 0.21; Mean = [ 1.15 6.69]; Std = [ 1.01 1.01]; Cluster 2: Probability = 0.21; Mean = [ 5.05 5.09]; Std = [ 0.72 0.83]; Cluster 3: Probability = 0.58; Mean = [ 2.17 2.06]; Std = [ 1.04 0.87];
3.- Iteración 2:
Cluster 1: Probability = 0.20; Mean = [ 1.05 6.86]; Std = [ 0.92 0.91]; Cluster 2: Probability = 0.23; Mean = [ 4.98 4.95]; Std = [ 0.75 0.89]; Cluster 3: Probability = 0.57; Mean = [ 2.08 2.04]; Std = [ 0.95 0.87];
4.- Iteración 3:
Cluster 1: Probability = 0.20; Mean = [ 1.01 6.88]; Std = [ 0.87 0.90]; Cluster 2: Probability = 0.24; Mean = [ 4.93 4.92]; Std = [ 0.78 0.93]; Cluster 3: Probability = 0.56; Mean = [ 2.06 2.02]; Std = [ 0.92 0.86];
5.- Iteración 4:
Cluster 1: Probability = 0.19; Mean = [ 0.99 6.88]; Std = [ 0.86 0.90]; Cluster 2: Probability = 0.25; Mean = [ 4.91 4.92]; Std = [ 0.79 0.94]; Cluster 3: Probability = 0.56; Mean = [ 2.05 2.02]; Std = [ 0.92 0.85];
6.- Iteración 5:
Cluster 1: Probability = 0.19; Mean = [ 0.99 6.88]; Std = [ 0.86 0.90]; Cluster 2: Probability = 0.25; Mean = [ 4.91 4.92]; Std = [ 0.80 0.94]; Cluster 3: Probability = 0.56; Mean = [ 2.05 2.01]; Std = [ 0.92 0.85];
7.- Iteración 6 y resultado final:
FINAL RESULT: Cluster 1 Number Points in Cluster: 195 Probability: 0.195195195195 Mean: [ 0.99752164 6.87917477] Standard Desviation: [ 0.85525541 0.90396413] Cluster 2 Number Points in Cluster: 248 Probability: 0.248248248248 Mean: [ 4.90529473 4.91753593] Standard Desviation: [ 0.79991193 0.94110496] Cluster 3 Number Points in Cluster: 556 Probability: 0.556556556557 Mean: [ 2.05069432 2.01442116] Standard Desviation: [ 0.92130407 0.85040552]
Para el resto de Data Sets tenemos los siguientes resultados pintados en 2 dimensiones:
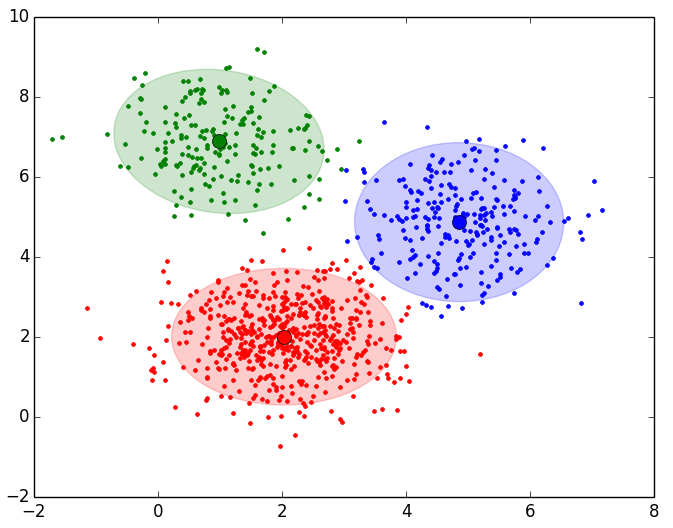
- Resultado final del EM para el Data Set 2 con 999 puntos y 3 Clusters:
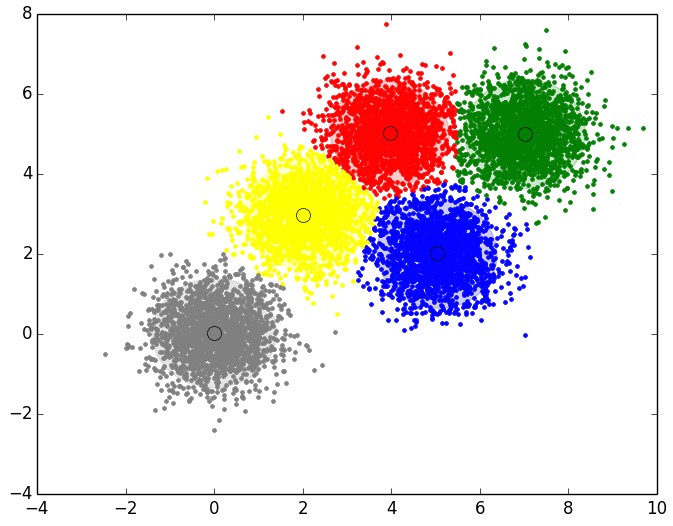
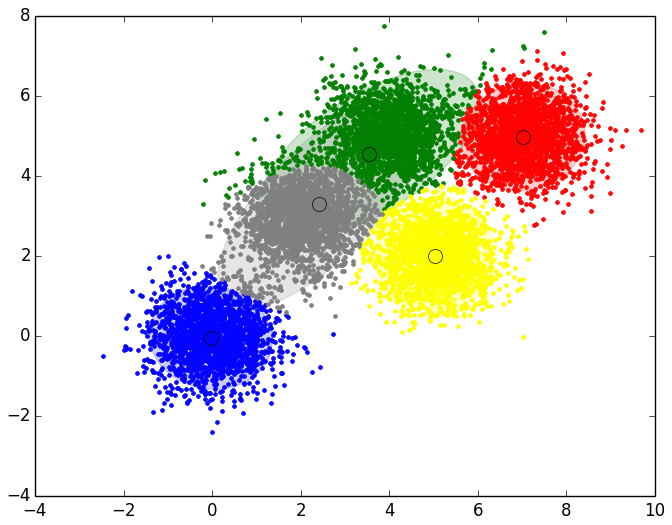
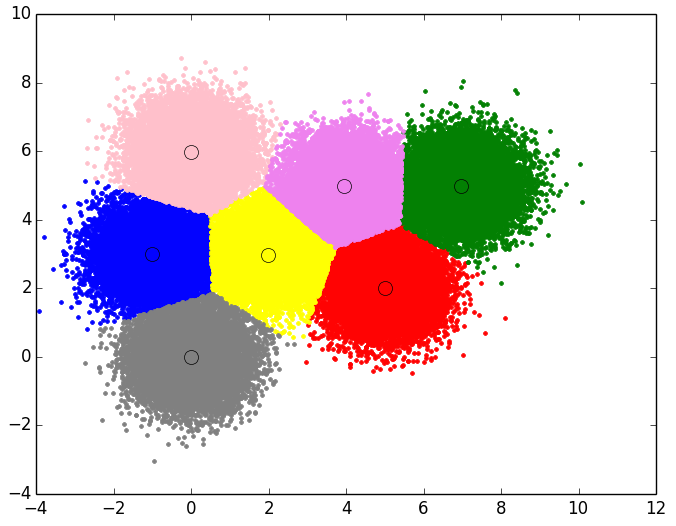
- Resultado final del EM para el Data Set 3 con 10000 puntos y 5 Clusters
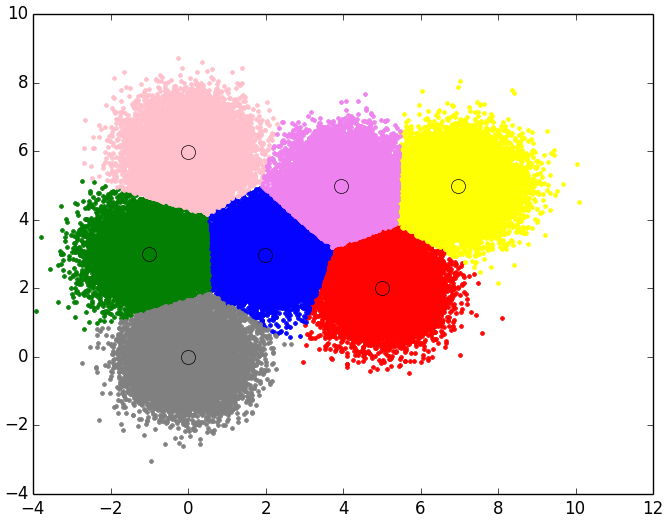
- Resultado final del EM para el Data Set 4 con 100000 puntos y 7 Clusters
Expectation-maximization (Gaussian mixture models) con scikit-learn
En la librería de “scikit-learn” esta implementado el Gaussian mixture models (GMM) que es el EM asumiendo distribuciones normales de probabilidad (o gaussianas); es decir, que los datos a Clusterizar se asume que han sido generados por distribuciones gaussianas, de ahí el nombre de “mezcla de modelos gaussianos”. Esta implementación del GMM, esta implementada de forma bastante optimizada, pudiendo ser ejecutado de diferentes formas en función de los parámetros que se le pase.
Dado que las librerías en general y esta de Machine Learning en particular evolucionan y son modificadas en el tiempo, no vamos a entrar a explicar cada uno de los parámetros que se le puede pasar al constructor de la clase sklearn.cluster.GMM() (para eso ya está la documentación de scikit-learn) pero si que vamos a mostrar aquellos parámetros que se consideran importantes para cualquier implementación del EM (o en esta caso del GMM).
En la versión 0.17 de la librería (última versión estable hasta la fecha de realización de este libro) el constructor de la clase GMM presenta los siguientes parámetros (si no se especifican tiene unos valores definidos por defecto):
class sklearn.mixture.GMM(n_components=1, covariance_type='diag', random_state=None, thresh=None,tol=0.001, min_covar=0.001, n_iter=100, n_init=1, params='wmc', init_params='wmc', verbose=0)
Como parámetros necesarios e importantes a especificar para que la ejecución del GMM sea correcta según el data set utilizado, debemos de definir correctamente los siguientes dos parámetros:
- n_components: Indicaremos el número de distribuciones normales (o Clusters) que queremos obtener para agrupar los objetos del data set.
- n_iter: número máximo de ejecuciones de los pasos de esperanza y maximización a realizar en el caso de que no converjan las medias de las distribuciones normales.
De forma opcional podemos definir una serie de parámetros con los valores que consideremos, siendo los más prácticos (según la opinión del autor) los siguientes:
- tol: Con este valor indicamos el umbral, tolerancia o margen de error para la convergencia.
- params: Le indicamos los parámetros que debe de actualizar en el paso de maximización.
Una vez construido el objeto de la clase GMM, debemos de llamar a los métodos pertinentes para que nos calcule los parámetros anteriormente indicados. En este caso y para el ejemplo que a continuación mostramos, vamos a llamar el método fit(x) al que pasamos como parámetro una lista de puntos (cada punto en un numpy array) y nos devuelve la probabilidad ‘π’ de pertenencia a las distribuciones normales (en el atributo weights_) y la media de las distribuciones normales (en el atributo means_). Por otro lado llamando al método predict(x); al que pasamos como parámetro una lista con los puntos del data set, nos calcula una lista alineada con la lista de puntos que le pasamos en el que nos dice a que distribución normal o Cluster pertenece cada punto.
A continuación mostramos el script completo en el que mostramos los resultados del GMM para uno de los 4 data sets:
# -*- coding: utf-8 -*-
__author__ = 'RicardoMoya'
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from sklearn.mixture import GMM
# Constant
DATASET1 = "./dataSet/DS_3Clusters_999Points.txt"
DATASET2 = "./dataSet/DS2_3Clusters_999Points.txt"
DATASET3 = "./dataSet/DS_5Clusters_10000Points.txt"
DATASET4 = "./dataSet/DS_7Clusters_100000Points.txt"
NUM_CLUSTERS = 3
MAX_ITERATIONS = 10
CONVERGENCE_TOLERANCE = 0.001
COLORS = ['red', 'blue', 'green', 'yellow', 'gray', 'pink', 'violet', 'brown',
'cyan', 'magenta']
def dataset_to_list_points(dir_dataset):
"""
Read a txt file with a set of points and return a list of objects Point
:param dir_dataset:
"""
points = list()
with open(dir_dataset, 'rt') as reader:
for point in reader:
points.append(np.asarray(map(float, point.split("::"))))
return points
def print_results(means_clusters, probability_clusters, label_cluster_points):
print '\n\nFINAL RESULT:'
for i, c in enumerate(means_clusters):
print '\tCluster %d' % (i + 1)
print '\t\tNumber Points in Cluster %d' % label_cluster_points.count(i)
print '\t\tCentroid: %s' % str(means_clusters[i])
print '\t\tProbability: %02f%%' % (probability_clusters[i] * 100)
def plot_ellipse(center, covariance, alpha, color):
# eigenvalues and eigenvector of matrix covariance
eigenvalues, eigenvector = np.linalg.eigh(covariance)
order = eigenvalues.argsort()[::-1]
eigenvector = eigenvector[:, order]
# Calculate Angle of ellipse
angle = np.degrees(np.arctan2(*eigenvector[:, 0][::-1]))
# Calculate with, height
width, height = 4 * np.sqrt(eigenvalues[order])
# Ellipse Object
ellipse = Ellipse(xy=center, width=width, height=height, angle=angle,
alpha=alpha, color=color)
ax = plt.gca()
ax.add_artist(ellipse)
return ellipse
def plot_results(points, means_clusters, label_cluster_points,
covars_matrix_clusters):
plt.plot()
for nc in range(len(means_clusters)):
# Plot points in cluster
points_cluster = list()
for i, p in enumerate(label_cluster_points):
if p == nc:
plt.plot(points[i][0], points[i][1], linestyle='None',
color=COLORS[nc], marker='.')
points_cluster.append(points[i])
# Plot mean
mean = means_clusters[nc]
plt.plot(mean[0], mean[1], 'o', markerfacecolor=COLORS[nc],
markeredgecolor='k', markersize=10)
# Plot Ellipse
plot_ellipse(mean, covars_matrix_clusters[nc], 0.2, COLORS[nc])
plt.show()
def expectation_maximization(dataset, num_clusters, tolerance, max_iterations):
# Read data set
points = dataset_to_list_points(dataset)
# Object GMM
gmm = GMM(n_components=num_clusters, covariance_type='full', tol=tolerance,
n_init=max_iterations, params='wmc')
# Estimate Model (params='wmc'). Calculate, w=weights, m=mean, c=covars
gmm.fit(points)
# Predict Cluster of each point
label_cluster_points = gmm.predict(points)
means_clusters = gmm.means_
probability_clusters = gmm.weights_
covars_matrix_clusters = gmm.covars_
# Print final result
print_results(means_clusters, probability_clusters,
label_cluster_points.tolist())
# Plot Final results
plot_results(points, means_clusters, label_cluster_points,
covars_matrix_clusters)
if __name__ == '__main__':
expectation_maximization(DATASET1, NUM_CLUSTERS, CONVERGENCE_TOLERANCE,
MAX_ITERATIONS)
A continuación pasamos a explicar detalladamente como hemos realizado el script. Todo el trabajo se realiza en el método expectation_maximization(dataset, num_clusters, tolerance, max_iterations) al que se le pasan como parámetros del data set, el número de Clusters, el umbral de convergencia y el número máximo de iteraciones. A este método le vamos a llamar desde el ‘main’, siendo los parámetros que se le pasan constantes definidas al principio del script:
# Constant
DATASET1 = "./dataSet/DS_3Clusters_999Points.txt"
DATASET2 = "./dataSet/DS2_3Clusters_999Points.txt"
DATASET3 = "./dataSet/DS_5Clusters_10000Points.txt"
DATASET4 = "./dataSet/DS_7Clusters_100000Points.txt"
NUM_CLUSTERS = 3
MAX_ITERATIONS = 10
CONVERGENCE_TOLERANCE = 0.001
COLORS = ['red', 'blue', 'green', 'yellow', 'gray', 'pink', 'violet', 'brown',
'cyan', 'magenta']
----------------------------------------------------------------------------------
if __name__ == '__main__':
expectation_maximization(DATASET1, NUM_CLUSTERS, CONVERGENCE_TOLERANCE, MAX_ITERATIONS)
Dentro del método expectation_maximization() empezamos leyendo los datos (puntos) del data set del que le indicamos, metiendo esos puntos en una lista de numpy arrays:
def expectation_maximization(dataset, num_clusters, tolerance, max_iterations):
# Read data set
points = dataset_to_list_points(dataset)
Inicializamos el objeto de la Clase GMM (de scikit-learn), pasándole como parámetros el número de Clusters (n_components), el umbral de tolerancia (tol) y número máximo de iteraciones (n_init) y los parámetros a actualizar en el paso de maximización (params):
gmm = GMM(n_components=num_clusters, covariance_type='full', tol=tolerance, n_init=max_iterations, params='wmc')
Llamamos al método fit(x) y al método predict(x); al que les pasamos la lista de puntos (numpy array), para que calculen los parámetros de las distribuciones y el Cluster al que pertenece cada punto:
# Estimate Model (params='wmc'). Calculate, w=weights, m=mean, c=covars gmm.fit(points) # Predict Cluster of each point label_cluster_points = gmm.predict(points)
Obtenemos los valores de la media de las distribuciones de los Clusters (means_clusters), la probabilidad de pertenencia a cada Cluster (probability_clusters) y la matriz de covarianzas (covars_matrix_clusters) que utilizaremos para pintar un área de dominio del Cluster:
means_clusters = gmm.means_ probability_clusters = gmm.weights_ covars_matrix_clusters = gmm.covars_
Por último implementamos dos métodos para imprimir por pantalla los resultados obtenidos (punto medio, número de puntos de cada Cluster y la probabilidad de pertenencia) y para pintar (con la librería matplotlib), los puntos medios y los puntos asignados a cada Cluster:
print_results(means_clusters, probability_clusters, label_cluster_points.tolist()) plot_results(points, means_clusters, label_cluster_points, covars_matrix_clusters)
Aplicando este script para los 4 data sets propuestos, tenemos los siguientes resultados:
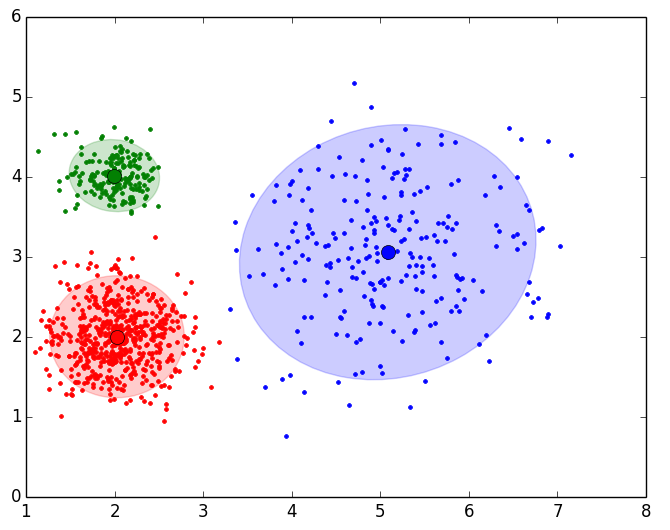
- Data Set 1: 3 Clusters y 999 puntos:
FINAL RESULT: Cluster 1 Number Points in Cluster 552 Centroid: [ 2.03233538 2.00853155] Probability: 55.061812% Cluster 2 Number Points in Cluster 253 Centroid: [ 4.85698668 4.87166594] Probability: 25.632025% Cluster 3 Number Points in Cluster 194 Centroid: [ 0.98302746 6.88925282] Probability: 19.306162%
- Data Set 2: 3 Clusters y 999 puntos:
FINAL RESULT: Cluster 1 Number Points in Cluster 186 Centroid: [ 1.99735203 4.01744321] Probability: 18.639301% Cluster 2 Number Points in Cluster 242 Centroid: [ 5.08393907 3.06038361] Probability: 24.320184% Cluster 3 Number Points in Cluster 571 Centroid: [ 2.02688227 2.00363213] Probability: 57.040515%
- Data Set 3: 5 Clusters y 10000 puntos:
FINAL RESULT: Cluster 1 Number Points in Cluster 1971 Centroid: [ 7.02380409 4.97477739] Probability: 19.503728% Cluster 2 Number Points in Cluster 1935 Centroid: [-0.03006596 -0.03848878] Probability: 18.591360% Cluster 3 Number Points in Cluster 2074 Centroid: [ 3.5474937 4.55700106] Probability: 19.963076% Cluster 4 Number Points in Cluster 2012 Centroid: [ 5.0348546 2.00442168] Probability: 19.923560% Cluster 5 Number Points in Cluster 2008 Centroid: [ 2.41381883 3.29885127] Probability: 22.018275%
- Data Set 4: 7 Clusters y 100000 puntos:
FINAL RESULT: Cluster 1 Number Points in Cluster 14270 Centroid: [ 5.00790293 2.00510173] Probability: 14.267490% Cluster 2 Number Points in Cluster 14219 Centroid: [-0.99805653 2.99389472] Probability: 14.217667% Cluster 3 Number Points in Cluster 14407 Centroid: [ 6.97099609 4.99667353] Probability: 14.545643% Cluster 4 Number Points in Cluster 14090 Centroid: [ 1.99643225 2.98306353] Probability: 13.934259% Cluster 5 Number Points in Cluster 14329 Centroid: [ 0.0083095 -0.00197396] Probability: 14.331673% Cluster 6 Number Points in Cluster 14366 Centroid: [ -4.37927760e-03 5.98768206e+00] Probability: 14.355278% Cluster 7 Number Points in Cluster 14319 Centroid: [ 3.940767 4.97634401] Probability: 14.347991%
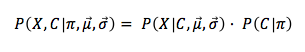
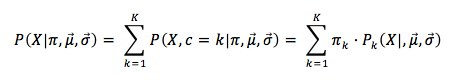
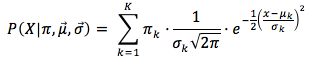
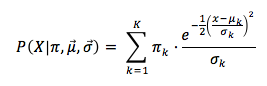
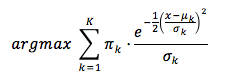
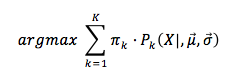




hola,
al probar tu codigo me arroja el siguiente error:
TypeError Traceback (most recent call last)
in
161 plot_results(clusters)
162
–> 163 expectation_maximization(DATASET3, NUM_CLUSTERS, ITERATIONS)
in expectation_maximization(dataset, num_clusters, iterations)
122 def expectation_maximization(dataset, num_clusters, iterations):
123 # Read data set
–> 124 points = dataset_to_list_points(dataset)
125
126 # Select N points random to initiacize the N Clusters
in dataset_to_list_points(dir_dataset)
17 with open(dir_dataset, ‘rt’) as reader:
18 for point in reader:
—> 19 points.append(Point(np.asarray(map(float, point.split(«::»)))))
20 return points
21
in __init__(self, coordinates)
6 def __init__(self, coordinates):
7 self.coordinates = coordinates
—-> 8 self.dimension = len(coordinates)
9
10 def __repr__(self):
TypeError: len() of unsized object
sabes como solucionarlo?
gracias por el contenido