Binario: Combinación y conversión
Conocer el sencillo funcionamiento de las «tablas de combinación» de los «sistemas de numeración» aportan una gran ventaja. Son necesarias para aprender a escribir cualquier número en dondequiera, en el momento más oportuno, y para realizar la conversión de cualquier valor que deseemos con unos simples cálculos (por ejemplo, desde o hacia el binario).
Puede que no sea el mayor orgullo del mundo, pero te aseguro que después de leer este artículo ya vas a ser capaz de entender chistes de informáticos como este:
Podría apostarme algo a que has visto este chiste en alguna de sus cientos de variantes que hay por Internet. Lo habrás escuchado en clase o en el trabajo, o de algún amigo aficionado a la tecnología. E incluso puede que se pasara por alto al no comprenderlo, aunque a partir de ahora tienes que entenderlo 😉
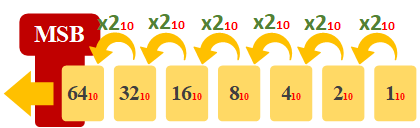
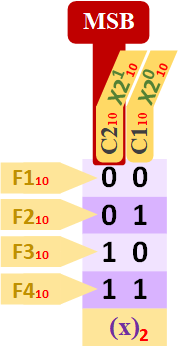
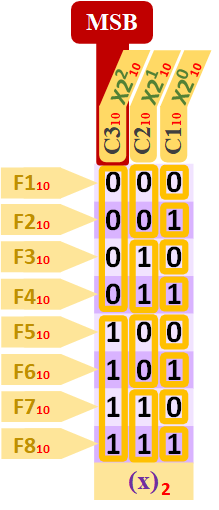
Te voy a revelar el truco del chiste, y mostrarte que es muy sencillo y muy rápido calcular de decimal a binario de cabeza. Mentalmente empieza en 1 y ve duplicando la cantidad hacia la izquierda tantas veces como la cantidad de bits tenga el número que quieras convertir de binario a decimal. Para el ejemplo de la mano anterior con calcular una vez el doble del primero nos vale (solo tenemos dos bits que representan los dos dedos levantados: “11” ).
Para el ejemplo me voy a pasar de veces (con dos de los dos bits nos valdría, el resto son sobrantes), voy a ir haciendo el doble del anterior (x2) varias veces de derecha a izquierda. Aunque también lo podrías hacer al revés (de izquierda a derecha), solo que es habitual calcular el binario de derecha a izquierda (Solo una cosa, a las siglas “MSB” de momento ni caso, en unas pocas líneas te lo explico; y los pequeños números en rojo puedes omitirlos por ahora, esos te los explico en la nota a continuación):
Nota sobre las bases en las imágenes de este artículo
Un recordatorio rápido de qué es una «base»: la base de un sistema de numeración (por ejemplo, “el sistema de numeración decimal” o “el sistema de numeración binario”) representa la cantidad de símbolo que tiene ese sistema de numeración (por ejemplo, para el decimal tiene los símbolos 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; o para el binario que tiene solo los símbolos: 0 y 1).
Como indicamos en el artículo del sistema de numeración binario, la base se pone como subíndice del número entre paréntesis, como por ejemplo “(1250)10”. Por motivos de diseño (por espacio y para no sobrecargar las imágenes de símbolos), en las imágenes lo voy a representar sin paréntesis y en color rojo, por ejemplo “125010”.
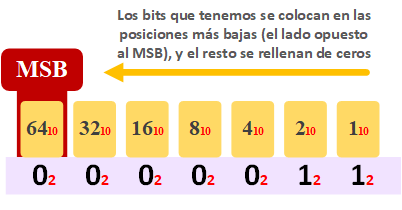
Debajo de los números antes calculados (…, 64, 32, 16, 8, 4, 2, 1), escribimos los bits del número binario empezando por el número más pequeño y hacia el más grande (del número binario “11” de los dedos de antes, escribimos el primer 1 debajo del 1, y el siguiente 1 debajo del 2). El resto rellenamos con ceros. Como en la siguiente imagen:
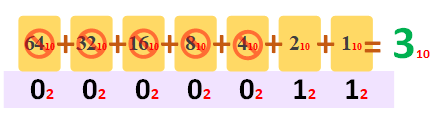
Y ahora solo nos queda calcular a decimal. Tachamos todos los múltiplos de 2 que tengan un “0” debajo y sumando los que tengan un “1” encima:
Por esto me he pasado, con el “2+1” me sobraría. Pero quería ponerte un ejemplo completo con “ceros” y “rellenado de ceros”.
Como ves, pillar el chiste informático es de cálculo inmediato (he tardado más en explicarlo que en hacer el cálculo de cabeza).
Pues si te digo que todo el tema de cálculo binario es así de simple puedes creértelo, no vamos a hacer nada “especial” o “extra”. Pero aprenderemos a tratar con números binarios muy grandes, sobre todo a saber sus significados y el porqué de las cosas.
Empecemos con el más fácil: las tablas de combinación en decimal (el resto de tablas son igual de sencillas, solo hay que entender la lógica y como hemos dicho, todo es igual).
Decimal (base 10)
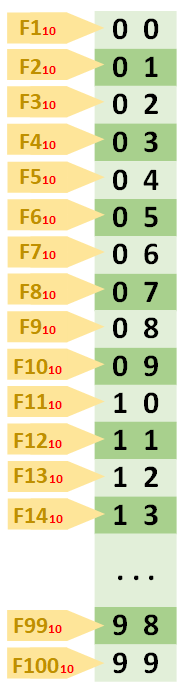
El sistema de numeración decimal, como sabemos solo tiene 10 símbolos (de base 10 que se compone de combinaciones de los diez símbolos que estamos más que acostumbrados: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Si los ponemos en una tabla todos los símbolos existentes decimales nos quedaría la siguiente:
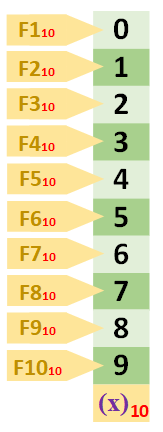
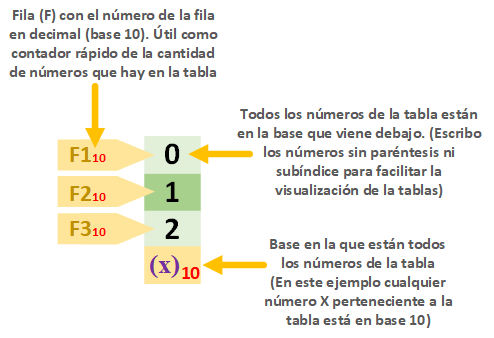
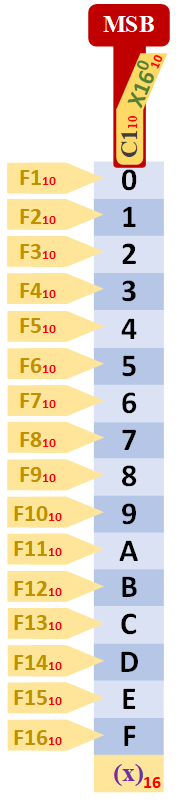
Leyenda de las tablas
Esta tabla es un poco especial (de diseño propio, para ver rápidamente algunas propiedades de una manera muy cómoda y completa). Hemos pintado todos los símbolos del sistema numérico para los dígitos que estamos viendo en vertical (con un fondo diferente para cada sistema de numeración, por ejemplo, para el decimal he elegido el verde). Debajo del todo está la base en la que están los números. A la izquierda la fila con el número (por simplificar he omitido algunos paréntesis de las bases) que principalmente la he puesto para contar los números que hay en la tabla (no te puedes fiar del número en sí para que ofrezca la respuesta directa a qué fila es, pues en la tabla anterior el primer número empieza en “cero”; después de la imagen explico esto más detalladamente).
Como puedes ver en este ejemplo, hay que tener en cuenta que el último número de la tabla va a ser uno menos que la cantidad de números. Es decir, el último número de la imagen anterior es el “2”, que es el tercer (F3) número de la tabla. Esto es debido a que empezamos a contar desde cero (0). Así que cuidado, porque si empezamos la cuenta en cero, el número final siempre será uno menos que la cantidad de números totales que hay en la tabla.
Si queremos representar números más grandes tenemos que añadir más dígitos (un dígito, o también llamado “cifra”, es cada símbolo en un número). Por ejemplo:
- El número 7 tiene 1 dígito
- El número 45 tiene 2 dígitos
- El número 897 tiene 3 dígitos
- El número 1.589 tiene 4 dígitos
- El número 18.897 tiene 5 dígitos
Por convención, cualquier número (da igual de que base) que tenga “ceros” a la izquierda no se escriben, es decir, el número “000000097” es igual que “97”. Y si el número tiene parte fraccionaria, no se escriben los ceros de la derecha; y el ejemplo, “000000097,150000” es igual a “97,15”.
Nota sobre la parte fraccionaria
La “parte fraccionaria” también se llama “parte decimal”, aunque no utilizo el término “parte decimal” en el artículo para no confundir con el “número decimal”.
Para evitar confusiones quiero indicar que represento la parte fraccionaria con “comas”, por ejemplo “3,141592”.
El punto lo utilizo para separar los “miles”, por ejemplo “2.000.000,78”.
Depende del país puede que lo utilizas al revés, simplemente cambia uno por otro 🙂
Recuerdo que la “parte fraccionaria” es aquella que no es la “parte entera” (también, la parte fraccionaria es la resta del número menos su “parte entera”). Es decir, del número “9.000,25” se divide en:
- Parte entera: 9.000
- Parte fraccionaria (9.000,25 – 9.000): 0,25
Parece que no, pero el cero delante se escriben en muchos sitios que seguro has visto, sobre todo donde hay huecos fijos para los números. Por ejemplo: un reloj digital (verás la hora como “07:09”), o las fechas de un sistema operativo (las podemos ver como “03/07/2017”), e incluso en boletos de lotería (que podemos ver como “0 0 5 7 6”), también en billetes de vuelos (por ejemplo “IBE 0467”), entre otros cientos de ejemplos. Como las tablas vamos a decir siempre los dígitos que van a tener los números, entonces los huecos son fijos siempre, por lo que siempre completaremos todas las posiciones del número con ceros a la izquierda. Además, al trabajar en binario siempre van a existir posiciones de tamaño fijo de memoria (es decir, cualquier archivo que tengas en tu ordenador siempre va a ocupar un múltiplo de bits dependiendo de dónde estén los bits, si en el procesador, el disco duro, la memoria RAM, etc. Por ejemplo, si el disco duro guarda de 8 en 8 bits, entonces un archivo siempre ocupará un múltiplo de 8 bits que es un 1 Bit como vimos en el artículo de unidades de medida de la información; por lo que dará igual que un archivo ocupe 75 bits, que en memoria siempre estarán reservados un múltiplo de 8 y siempre dirá que hay 80 bits ocupados ¿y si el archivo crece a 81 bits? Pues ocupará 88 bits) y es otra razón por la que poner ceros en la parte que no modifican el valor para completar.
Eso está muy bien, pero si queremos escribir la tabla con todas las combinaciones de todos los números decimales que tengan dos dígitos no vale con pintar del “diez” (10) al “noventa y nueve” (99), también del “cero” (0) al “nueve” (9), pues su primer dígito es un “cero” que no se suele escribir (por ejemplo, para el símbolo “5” representado con dos decimales se escribe “05”). Quedaría la siguiente tabla:
Otra cosa importante -de cualquier número del sistema de numeración que queramos- es conocer el orden a leer los símbolos de números con varios dígitos. Si te escribo “12” y te pregunto ¿qué número decimal es? Seguramente me digas “doce”, pero si se lo pregunto a alguien que los lea al revés me dirá “veintiuno”. Por lo que es importante conocer qué digito es el:
- Dígito más representativo: el dígito de mayor valor.
- Dígito menos representativo: el dígito de menor valor.
Por ejemplo, si queremos leer el número “2.017” sabemos que el “Dígito más representativo” (en la imagen lo he representado con “D+R”) está a la izquierda del todo que es donde están los “miles”, y el “Dígito menos representativo” (representado en la siguiente imagen como “D-R”) está al lado contrario, a la derecha del todo, que serán las unidades. De este modo podemos leer “2.017” como “Dos mil diecisiete” (y no al revés como “Siete mil ciento dos”).
Basta con conocer donde se ubica el “Dígito más representativo” para deducir dónde está el “Dígito menos representativo” (si uno está al principio del número, el otro estará al final; y viceversa). Por lo que normalmente se suele mencionar siempre al “más representativo”, y se deduce el “menos representativo”.
Por fortuna y por convención, para los números decimales el “Dígito más representativo” está siempre en el dígito de más a la izquierda. Entender esto es importante para cualquier sistema de numeración (sobre todo para el sistema binario donde sí puede variar si se lee de izquierda a derecha o de derecha a izquierda).
Del anterior ejemplo “2.017” de cuatro dígitos, sabiendo que el “Dígito más representativo” es el dígito de más a la izquierda, si te pregunto:
- ¿Qué dígito son los millares (los “miles”)? Ya me puedes decir que es donde está el “Dígito más representativo”, el dígito de la izquierda del todo, el primer dígito comenzando por la izquierda
- ¿Qué dígito son las centenas? El segundo dígito empezando por la izquierda
- ¿Qué dígito son las decenas? El tercer dígito empezando por la izquierda
- ¿Qué dígito son las unidades? El cuarto dígito empezando por la izquierda
Unidades, centenas, decenas, millares, etc. Quiere decir que puedo multiplicar cada dígito del número “2.017” por la potencia de la base, en este caso potencia de 10 (potencia de “diez” porque el decimal es base “diez”), estando ubicado el “Dígito más representativo” en la potencia de 10 mayor (y el “Dígito menos representativo” en la potencia de 10 menor, “el elevado a cero”):
- Millares: 2 x 103 = 2 x 1.000 = 2.000
- Centenas: 0 x 102 = 0 x 100 = 0
- Decenas: 1 x 101 = 1 x 10 = 10
- Unidades: 7 x 100 = 7 x 1 = 7
Cuanto menos curioso, que si sumo todos los resultados me da el número “2.017”:
2.000 + 0 + 10 + 7 = 2.017
Conocer cuál es el “dígito más representativo” nos viene bien para establecer los múltiplos que luego nos ayudarán en la conversión entre sistemas de numeración (sobre todo de cualquier sistema de numeración al decimal).
Leyenda de las tablas (Ampliación)
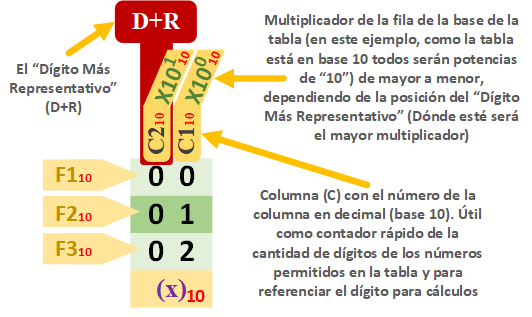
Antes hemos visto las filas (F) de la tabla, ahora les toca el turno a las columnas (C).
Marcaremos con “D+R” a la columna del “Dígito más representativo”.
Teniendo este dato, empezaremos por la columna opuesta al “Dígito más representativo” (en el siguiente ejemplo la de la derecha del todo) a numerar desde el 1 -como “C1”- hasta el total de las columnas que haya en la tabla (en este ejemplo solo hay 2 columnas -la última será “C2”). La numeración de las columnas nos servirá para contar los dígitos y poder hacer referencia a un número en concreto (semejante al juego de cuadrícula de “Hundir la flota”, podremos decir en “C1” y “F3” hay un “2”).
Además, las columnas nos ayudarán a ubicar los múltiplos de la base.
Es importante diferenciar claramente los números que aparecen en las tablas (para evitar confusiones, llamo “valor” al número dentro de la tabla; es decir, a los que están sobre fondo verde en las imágenes de estas tablas):
- Cantidad de dígitos que tiene como máximo un valor en la tabla (Las columnas de la tabla).
- Cantidad total de valores que hay en una tabla (Las filas de la tabla). Es lo mismo que la cantidad de combinaciones posibles que podemos hacer con la cantidad de dígitos elegidos.
- Valores con los que empieza y termina la tabla (así como los que componen el resto de la tabla, que son muy deducibles). Estos valores son los números en la base que queramos. Nota: Como dijimos, si el primer valor empieza en cero, cada valor será siempre uno menos que la fila correspondiente de la tabla (uno menos que la cantidad de números que llevemos contados hasta ese valor)
- Base en la que están los valores de la tabla
- Multiplicador decimal en potencias de ayuda para las conversiones (las veremos en detalle más adelante)
La tabla completa del sistema de numeración decimal para cuatro dígitos sería (es sencilla, tiene tres cosas que se repiten en todas las tablas, échale un vistazo y continuamos):
Ejemplo comparativo de conversión
Y terminamos con un ejemplo completo para “convertir” el número decimal “3908” al mismo sistema decimal (aquí no se convierte nada, pero cuando pasemos a la siguiente base entenderás porque hacemos esta “conversión así mismo”):
- El número decimal para convertir a decimal: 3908
- Para cada columna su multiplicador decimal: (3 x 103) + (9 x 102) + (0 x 101) + (8 x 100)
- Cada potencia es: (3 x 1.000) + (9 x 100) + (0 x 10) + (8 x 1)
- Calculamos los paréntesis: 3.000 + 900 + 0 + 8
- Sumamos: 3908
- Conversión: (3908)10 = (3908)10
Binario (base 2)
Al fin llegamos a lo bueno, a las “tablas binarias” después de entender las anteriores “tablas decimales”.
Como ya dijimos los números de un sistema binario solo tienen dos símbolos (pues es base 2): el uno (1) y el cero (0).
Como en informática no trabajamos con “números” sino con bits, no se nombra a cada símbolo de un número binario como “dígito” (ni tampoco como “cifra”) sino como “bit”, por lo que en binario decimos (es lo mismo con otro nombre):
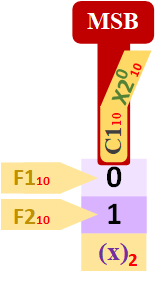
- Bit más representativo (MSB, del inglés “Most Significant Bit”): el bit de mayor valor (equivale al “Dígito más representativo”, al “D+R”).
- Bit menos representativo (LSB, del inglés “Less Significant Bit”): el bit de menor valor (equivale al “Dígito menos representativo”, al “D-R”).
Para dibujar la tabla con un solo bit sería muy simple:
Como solo tiene “0” y “1”, pues solo tiene dos filas. Hemos dicho que es de un solo bit tan solo tiene una columna. Y el multiplicador decimal recuerda que es la potencia (es la base del sistema de numeración que tratemos). En este caso el binario es base 2, por lo que la potencia es 2.
La tabla más simple con dos bits quedaría:
¿Cómo colocar los “0s” y “1s” en cualquier tabla para cubrir todas las combinaciones posibles?
Como vimos, los sistemas de numeración tienen símbolos finitos, por lo que cada vez que terminemos los símbolos de un dígito (por ejemplo, en decimal sus símbolos terminan en 9, y luego se agrupan para empezar otra vez con los símbolos desde el 10, 11, 12, etc.), incrementamos en uno el siguiente de más a la izquierda (bien dicho: se incrementa el más cercano al “Dígito más representativo”), y se vuelve a empezar con el primer símbolo. Así hasta cubrir todos los dígitos de la tabla.
Un truco rápido para pintar la tabla en binario para cualquier número de bits.
Primero, hay que calcular la cantidad combinaciones diferentes de números (Filas) que va a tener la tabla, es fácil conociendo la cantidad de dígitos (bits, Columnas) que va a tener la tabla, se calcula con la potencia del número de la base (esto de calcular la “cantidad de números de una tabla” también funciona para cualquier otro sistema de numeración).
Por ejemplo, si queremos construir la tabla binaria de 3 bits de tamaño para el sistema de numeración binario (que es base 2):
23 = 8
Es decir, la tabla binaria para 3 bits va a contener exactamente 8 números (8 Filas) diferentes.
Segundo, elegimos una columna para empezar, la de más a la izquierda o la de más a la derecha (normalmente se elige la del “bit más representativo”, aunque es indiferente). Y empezamos (recomiendo ir siguiendo la tabla de debajo de la columna desde más a la izquierda hacia la derecha):
- La primera columna la rellenamos una mitad de “ceros” y la otra mitad de “unos”. Por ejemplo, para la tabla de 3 bits en binario los cuatro primeros serían “ceros” y los cuatro restantes “unos”, quedaría la columna (en vertical): 00001111
- La segunda columna la rellenamos con la mitad de los de antes, salteándolos. Siguiendo con el ejemplo, antes rellenamos de “cuatro en cuatro” (cuatro “ceros” y luego cuatro “unos”), ahora la mitad de antes es “dos en dos” (dos “ceros” y luego dos “unos”, indefinidamente hasta rellenar la tabla), quedaría esta columna: 00110011
- El resto de columnas es igual, siempre van a saltarse siendo la mitad de la anterior, la última columna terminara siendo siempre los dos símbolos salteados: 0, 1, 0, 1, 0, 1, etc. Para la tercera columna la mitad de la segunda (que era de “dos en dos”), ahora es de “uno en uno”, quedando la columna: 01010101
Ya sabemos dibujar absolutamente todas las combinaciones (fíjate que con esto tenemos todas las filas con combinaciones de números únicos, sin repetir en otras filas; además, ordenados de menor a mayor) de cualquier tabla binaria (de cualquier cantidad de columnas) en cuestión de segundos.
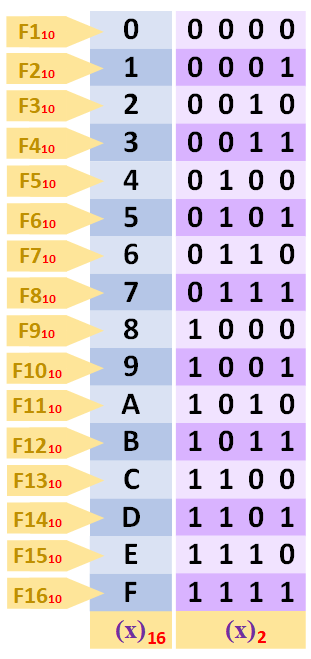
Entonces la tabla para cuatro bits quedaría:
Ya tenemos las tablas, ahora veamos cómo convertir un número binario a decimal.
Es importante entender bien la relación de las columnas de las tablas binarias con sus multiplicadores decimales (entender la lógica y poder utilizarse en cualquier momento), pues con ellas conseguiremos rápidamente convertir cualquier número binario a decimal de cabeza. Las potencias de dos las repasamos en un segundo:
- 20 = 1
- 21 = 2
- 22 = 4
- 24 = 8
- …
- 2n
Por lo que, de cualquier número de columnas podemos saber cuál es su valor tanto en formato de potencia como directamente el número decimal con nuestra mente, en cuestión de segundos:
Si te fijas en el primer ejemplo del chiste informático del principio del artículo, es como calculamos los multiplicadores decimales de las columnas.
Por cierto, los estoy llamando “multiplicadores decimales” porque nos sirven para convertir cualquier número de la tabla (de la base) que estemos utilizando a decimal, simplemente con sumar.
Conversión de binario a decimal
Ahora, sí te pregunto ¿Cuánto es el número binario “1011” en decimal? Pues sencillo, de manera semejante a como lo calculamos la conversión anterior de “decimal a decimal” (está arriba, en el apartado llamado “Ejemplo comparativo de conversión”). “1011” tiene cuatro bits (cuatro dígitos), y como queremos escribirlo en decimal los “unos” y “ceros” serán decimales, por lo que podemos calcularlo por pasos:
- El número binario para convertir a decimal: 1011
- Para cada columna su multiplicador decimal: (1 x 23) + (0 x 22) + (1 x 21) + (1 x 20)
- Cada potencia es: (1 x 8) + (0 x 4) + (1 x 2) + (1 x 1)
- Calculamos los paréntesis: 8 + 2 + 1
- Sumamos: 11
- Conversión: (1101)2 = (11)10
Muy fácil y extremadamente sencillo. El binario “1011” es 11 en decimal. Ya sabes cómo calcular del binario al decimal.
Aclaración extra
Aunque aquí estoy pintando las filas (Fx) para saber la cantidad. Como ya se indicó, hay que tener cuidado con no confundir cantidad de valores con el último valor de la tabla. En binario se rellenan desde la primera combinación de todos ceros (“000…000”), pasando por todas las combinaciones, y terminando con el todo unos (“111…111”).
Por ejemplo, antes hicimos el ejemplo para construir la tabla de 3 bits, vimos que la cantidad de valores en la tabla eran 8 (23 = 8). Donde el primer valor binario es “000” (que representa al “0” decimal), y el último el “111” (que representa la “7” decimal). Puede surgir la confusión de pensar que el último valor representa al “8” decimal al ser el último en la tabla, pues la cantidad de valores en la tabla son “8” y esto no es cierto por culpa de empezar en cero el primer valor (recuerda que, si empieza en cero el primer valor en la tabla siempre va a ser uno menos todos los valores respecto a la fila; y el último valor va a ser la cantidad de valores en la tabla menos uno).
Hay que diferenciar el multiplicador decimal de cada columna del cálculo para contar la cantidad de números en una tabla que es la base, elevado a la cantidad de dígitos (columnas) que tiene un número. Como por ejemplo para la tabla de cuatro dígitos (que empieza en “0000” y termina en “1111”), será 24 = 16 números en la tabla (el primer valor en la tabla en decimal representa al “0” y el último al “15”). Inducir al ERROR pensar que el último multiplicador decimal es la cantidad de valores en la tabla, es el mismo problema de antes al empezar el primer valor en cero. Para la tabla binaria de 4 dígitos, el último multiplicador mayor es 23 que es 8 y no 16 que sería la cantidad de valores; esto es así para que se cumpla la conversión del último valor de la tabla “1111”:
- El número binario para convertir a decimal: 1111
- Para cada columna su multiplicador: (1 x 23) + (1 x 22) + (1 x 21) + (1 x 20)
- Cada potencia es: (1 x 8) + (1 x 4) + (1 x 2) + (1 x 1)
- Calculamos los paréntesis: 8 + 4 + 2 + 1
- Sumamos: 15
- Conversión: (1111)2 = (15)10
Conversión de decimal a binario
¿Y para convertir un número decimal a binario, por ejemplo, el número “53” decimal a binario? Se puede decir que es lo mismo que antes, pero a la inversa, necesitamos buscar el mayor multiplicador de las columnas que al restar el número decimal el resultado sea un número positivo o cero (si es cero quiere decir que hemos acabado), entonces será “1” binario; sin embargo, si da un resultado negativo, será “0” binario. Veamos los pasos del ejemplo (me voy a explayar un poco con la siguiente explicación, pero es bastante sencillo, es todo el rato restar el multiplicador de las columnas al resultado positivo):
- El número decimal para convertir a binario: 53
- Buscamos el primer mayor multiplicador que al restar a 53 siga siendo positivo, por ejemplo, 128 (= 27) será “0” binario pues al restarlo da un número negativo (53 – 128 = -75), lo mismo ocurre con 64 (= 26) que da negativo (53 – 64 = -11) que también será “0” binario.
- La primera columna que es la mayor que da como resultado un “1” binario es 32 (= 25) que corresponde con la sexta columna (C6): 53 – 32 = 21, el resultado positivo por lo que es 1 Como hemos utilizado el 32 = 25 (ver imagen de las columnas anterior) sabemos que pertenece a la sexta columna (C6), y desde aquí continuamos con el resto de columnas hacia abajo.
- 16 (= 24) de C5: 21 – 16 = 5, resultado positivo por lo que es 1 binario, para la sexta columna (C6)
- 8 (= 23) de C4: 5 – 8 = -3, resultado negativo por lo que es 0 binario (el resultado negativo no se tiene en cuenta para el siguiente multiplicador inferior, se reutiliza el anterior resultado positivo)
- 4 (= 22) de C3: 5 – 4 = 1, resultado positivo por lo que es 1 binario
- 2 (= 21) de C2: 1 – 2 = -1, resultado negativo por lo que es 0 binario
- 1 (= 20) de C1: 1 – 1 = 0, resultado cero por lo que es 1 binario y hemos acabado
- Recopilamos los 1s y 0s binarios en orden de las columnas (por el MSB): 110101
- Entonces: (110101)2 = (53)10
Ejemplo comparativo
Podemos equiparar esta forma de calcular a cuando una máquina (un cajero automático o una máquina de cambio) te tiene que dar dinero. La máquina te intentará dar la moneda del mayor valor del total que te tenga que dar, sino puede intentará con la siguiente; siempre irá intentando con la siguiente más pequeña para darte la menor cantidad de monedas, y así darte todo el dinero.
Supongamos que quieres que una máquina te de 6€; dicha máquina tiene en su interior billetes de 10€, billetes de 5€, monedas de 2€ y monedas de 1€. El funcionamiento será intentar darte un billete de 10€ pero se pasa (6 – 10 = -4, sale un resultado negativo), luego probará con el billete de 5€ con lo que puede darte el billete por estar contenido en 6€ (6 – 5 = 1, por lo que le falta por darte 1€), luego una moneda de 2€ pero no lo conseguirá (1 – 2 = -1, que es negativo), como solo queda la moneda de 1€ te la dará (1 – 1 = 0). De esta manera te habrá devuelto un billete de 5€ y una moneda de 1€, lo que es lo mismo que:
0x10 + 1×5 + 0x2 + 1×1 = 6
Si te fijas es exacto a lo que hemos hecho para calcular el número decimal desde el binario.
Por cierto, esta manera inteligente de conseguir el resultado deseado se denomina “algoritmo voraz” (más información en https://es.wikipedia.org/wiki/Algoritmo_voraz ) 😉
Existen otras maneras para convertir un binario a un decimal. Creo que esta es la más sencilla y la más rápida de ejecutar de cabeza.
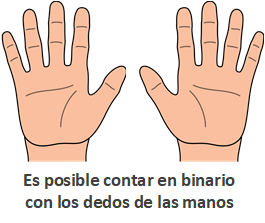
Curiosidad: ¿Cuántos números binarios podemos representar con los dedos de las manos?
Es posible contar en binario con los dedos de las manos. Por ejemplo, si el dedo está hacia arriba sería un 1 binario, y si está doblado sería un 0 binario.
Basándonos en lo que vimos antes te recomiendo que hagas el cálculo como práctica (mentalmente puedes hacer el cálculo lógico).
Como tenemos diez dedos (cinco por cada una de las manos), tendríamos 10 dígitos (que es lo mismo a 10 columnas, columnas de las tablas de antes), que equivale a números de tamaño de 10 bits. Por tanto, la cantidad de números que hay en la tabla es (repaso: la base del sistema de numeración elevado a la cantidad de dígitos que tiene el número; en este caso en binario la base es 2, y 10 bits son los 10 dígitos):
210 = 1.024
Es decir, con los dedos de las manos podemos contar hasta ¡1.024 posibles números! ¡Increíble que podamos contar hasta más de mil con tan pocos dedos de las manos! 😀
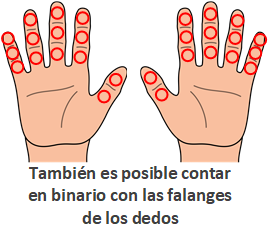
Ya puestos, en el anterior artículo de sistema de numeración mencioné la curiosidad de como contaba la antigua Mesopotamia en base 60 con las falanges de los dedos. Si modificamos un poco la forma de realizar la cuenta y…
¿Y si utilizáramos todas las falanges de los dedos para contar en binario?
Si miras las palmas de tus manos y cuentas las falanges que hay en todos tus dedos (recuerdo que las falanges son las partes separadas del dedo divididas por donde se dobla el mismo dedo). Podríamos marcar con un boli las falanges ocupadas que representarían un 1 binario, o desocupadas que serían el 0 binario.
Tenemos catorce falanges por mano, que por dos son 28 falanges totales (lo que serían 28 dígitos). Como antes, calculando la cantidad de combinaciones posibles (la cantidad de números que podemos contar con los dígitos que disponemos), resulta que son:
228 = 268.435.456
Con nuestras manos podemos contar casi ¡doscientos setenta millones de números! ¡Todavía mucho más increíble que podamos contar tal salvajada de millones tan solo con los dedos de nuestras manos!
Sobre los posibles usos de un mísmo número binario
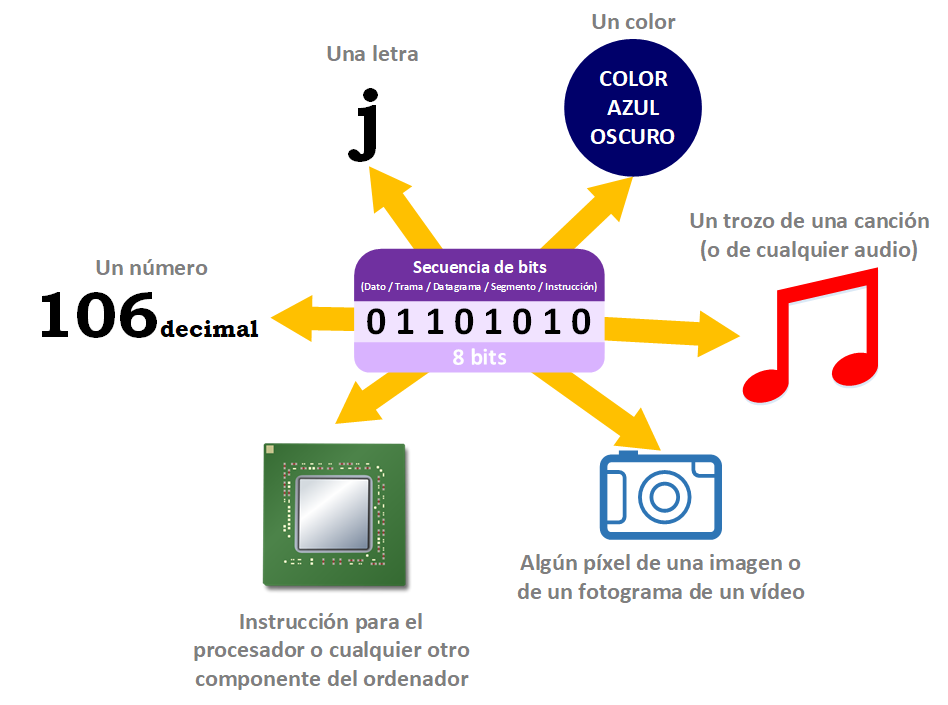
¿Recuerdas al principio del anterior artículo de sistema de numeración cuándo te dije que un número binario puede significar cualquier cosa?
Puse de ejemplo el número binario “01101010” que era el “106” en decimal. Con lo ya explicado ya tienes resuelto el primer enigma. Puedes calcular de decimal a binario y viceversa: (01101010)2 = (106)10
Hexadecimal (base 16)
El Hexadecimal, es base 16 y por ello este sistema de numeración tiene dieciséis símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Trabajar con binario está muy bien, pero no es cómodo para “comprar y llevar”. Es un número muy feo con tantos “unos” y “ceros”, además de muy largo ¿Recuerdas cuando te decía en el anterior artículo de sistema de numeración que el número binario “01101010” podría representar otras cosas, como el color “Azul Oscuro” (ver anterior nota: “Nota sobre las posibles representaciones de un número binario”)? Y es azul oscuro en el modelo de color RGB.
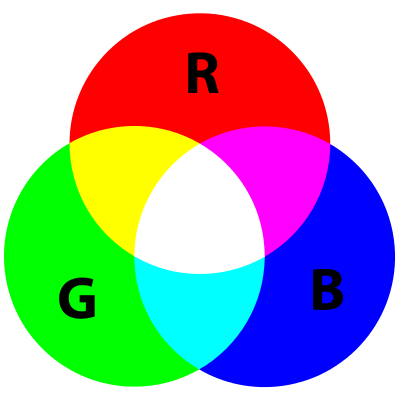
Modelo de color RGB
Aunque existen varios modelos de color, el más utilizado es el RGB (“Rojo Verde y Azul”, del inglés “Red Green Blue”. Información completa en https://es.wikipedia.org/wiki/RGB).
Que se basa en lo que dimos en el colegio sobre los colores primarios de la luz (“un color primario de la luz” es aquel color que no es mezcla de ninguno) y es el modelo que nuestros ojos utilizan para informar al cerebro de los colores. Y lo utilizan prácticamente todas las pantallas que puedas imaginarte (televisiones, monitores de PC, Tablets, Smartphones, etc.). Como entenderás, cada pixel de una imagen contiene esta información de color (además de la posición, entre otra información). Es decir, una imagen es un buen montón de bits (y ya no hablemos de un vídeo que no solo son muchas imágenes, sino que también tiene audio 😉 )
El modelo RGB utiliza 24 bits (8 bits para el Rojo + 8 bits para el Verde + 8 bits para el Azul) para representar un color.
Por ejemplo, la secuencia de bits que hemos visto en otros ejemplos “01101010” quedaría con 24 bits como (rellenamos de ceros hacia la izquierda lo que falte hasta 24 bits):
Como hemos visto anteriormente, 8 bits pueden albergar hasta 256 combinaciones de números binarios (empezando en “00000000” binario que es el “0” decimal y terminando en “11111111” que es el “255” decimal). Es decir, vamos a tener 256 combinaciones de color Rojo, 256 de Verde y 256 de Azul. El valor más pequeño (el “00000000”) es el negro puro y el mayor el color más vivo (el “11111111”).
Por sencillez (y por practicidad) los colores se expresan en otras bases, como la decimal, como:
rgb(“cantidad de ROJO”, “cantidad de VERDE”, “cantidad de AZUL”)
Por ejemplo, para el color azul oscuro que hemos visto de binario “01101010” y que es “106” en decimal, quedaría como:
rgb(0, 0, 106)
Con esto podemos jugar con las mezclas, que nos dará como resultado el resto de colores. Por ejemplo, “rojo y verde” vivos es “amarillo” vivo (puedes ver cómo queda la mezcla en la anterior imagen con los tres círculos de color):
rgb(255, 255, 000)
Por otro lado, el hexadecimal lo verás muchísimo también, pues es muy fácil de agrupar al ser una potencia de 2. Así será como veras los colores en todas las calculadoras de colores (calculadoras online o de los mismos programas de edición de imágenes), así como al programar con colores. Para expresar un color en hexadecimal (y como vimos en el artículo anterior de sistemas de numeración) se antepone el símbolo almohadilla “#” al número. De este modo tenemos por ejemplo que (Poco más adelante, veremos cómo utilizar el hexadecimal, aquí solo te lo muestro como adelanto):
- binario “00000000 00000000 00000000” = decimal “rgb(0, 0, 0)” = hexadecimal “#00 00 00”
- binario “11111111 11111111 11111111” = decimal “rgb(255, 255, 255)” = hexadecimal “#FF FF FF”
Mira la imagen a continuación y responde a la siguiente pregunta ¿Qué número es más sencillo y rápido de memorizar/transportar/escribir el binario o el hexadecimal?
Y lo mismo si quitamos los ceros “inútiles” de la izquierda tendríamos: “(1101010)2 = (6A)16”. Es mucho más corto utilizar el hexadecimal que el binario. Este truco para acortar el número binario (realmente el truco es convertir el número a otra base superior para comprimir números muy grandes de bases inferiores) se utiliza mucho con las bases que sean potencias de 2. No es raro que te encuentres por cualquier lado (Internet, libros, etc.) secuencias de bits escritas en bases como el cuaternario (base 4), el octal (base 8), el hexadecimal (base 16), en base 32, en base 64, etc. En cualquier base menos en binario (base 2).
El número hexadecimal (base 16) consta de 16 símbolos. Se escogieron del 0 al 9 y para los restantes de la letra “A” a la “F”. La tabla de todos los símbolos existentes hexadecimales:
Esta tabla es bastante más grande, si te fijas sigue los mismos principios que las anteriores bases: que es fácil de crear.
Rápidamente te muestro la tabla de cuatro dígitos para el hexadecimal:
Conversión de hexadecimal a decimal
La conversión de hexadecimal a decimal igual que la de binario. Por ejemplo, para convertir el número hexadecimal “7C0A” a decimal:
- El número hexadecimal para convertir a decimal: 7C0A
- Para cada columna su multiplicador decimal: (7 x 163) + (C x 162) + (0 x 161) + (A x 160)
- Sustituimos cada símbolo hexadecimal (las letras) por los decimales: (7 x 163) + (12 x 162) + (0 x 161) + (10 x 160)
- Cada potencia es: (7 x 4.096) + (12 x 256) + (0 x 16) + (10 x 1)
- Calculamos los paréntesis: 28.672 + 3.072 + 0 + 10
- Sumamos: 31.754
- Conversión: (7C0A)16 = (31.754)10
Conversión de hexadecimal a binario
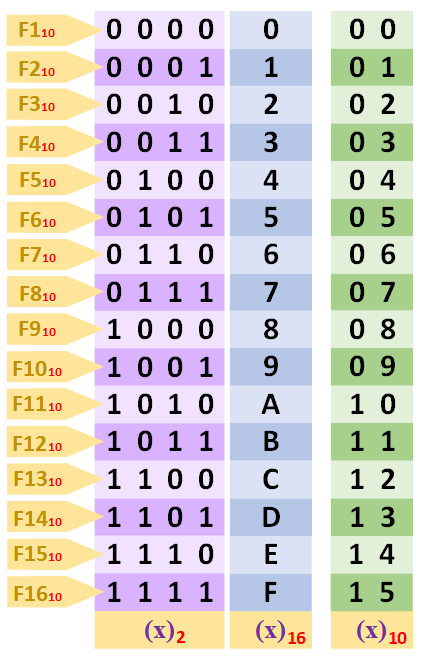
La comparación del hexadecimal con el decimal y el binario la podemos ver en la siguiente tabla:
Interesa sobre todo que la tabla hexadecimal se repite justo cuando acaba la de binario de 4 bits (debido a que 16 es una potencia de 2, concretamente 24 = 16; cualquier base que sea potencia de 2 se repetirá y será muy buena para convertir inmediatamente cada símbolo a su binario). Con ella es sencillo de convertir cada símbolo hexadecimal a un grupo de 4 bits directamente con la tabla (quito el decimal para no liar, pues el decimal al no coincidir con el fin de la tabla hexadecimal no se puede utilizar para convertir el símbolo hexadecimal a decimal):
Convertir de hexadecimal a binario es muy simple. Basta con convertir cada letra del hexadecimal a binario por separado. Por ejemplo, para convertir el número hexadecimal “7C0A” a binario:
- El número hexadecimal para convertir a binario: 7C0A
- Sustituir cada símbolo hexadecimal por su binario: 0111 1100 0000 1010
- Conversión: (7C0A)16 = (0111110000001010)2
Conversión de binario a hexadecimal
Y al revés, convertir de binario a hexadecimal es lo mismo que antes. Cada grupo de cuatro bits es un símbolo hexadecimal. Por ejemplo, para convertir el número binario “0111110000001010” a hexadecimal:
- El número binario para convertir a hexadecimal: 0111110000001010
- Separar en grupos de cuatro bits: 0111 1100 0000 1010
- Sustituir cada grupo por su símbolo hexadecimal: 7C0A
- Conversión: (0111110000001010)2 = (7C0A)16
Conversión del hexadecimal a cualquier sistema de numeración
Teniendo el valor en binario podemos convertir el valor a decimal (como vimos anteriormente) o en la base que queramos.
Codificación de los textos
También dijimos que un grupo de bits podría ser una letra (como se ha recordado en este artículo y se dejó la incógnita en el anterior de sistemas de numeración). Pusimos de ejemplo que el número binario “01101010” (o el hexadecimal “6A”) es la letra “j” (la jota minúscula).
Al igual que con los colores hay varios estándares. Uno muy famoso es el ASCII (“Código Estándar Americano para el Intercambio de Información”, del inglés “American Standard Code for Information Interchange”. Información completa en ASCII https://es.wikipedia.org/wiki/ASCII ). Donde se utilizan 8 bits para guardar cada símbolo (símbolos como las letras del abecedario, los diez símbolos de los números decimales, @, +, -, /, etc.).
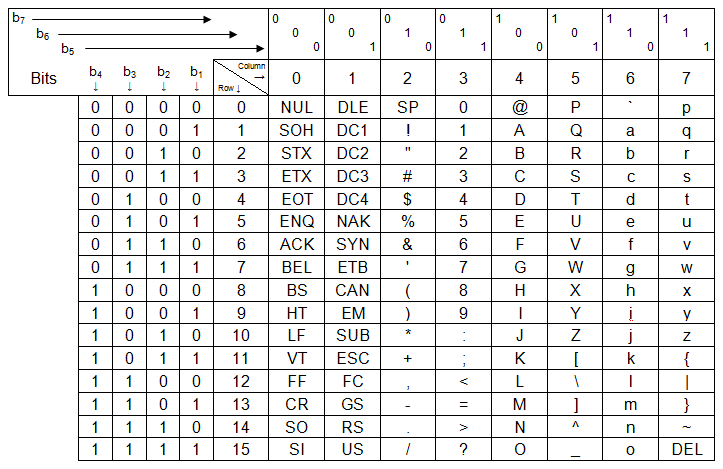
Simplemente se basa en sustituir un código binario por un símbolo del siguiente “Gráfico de Código ASCI 1968”:
Parece complicado, pero es muy sencillo. El gráfico ofrece tanto la conversión binaria (en el cuadro de arriba a la izquierda donde pone “b7”, “b6”, “b5”, “b4”, “b3”, “b2”, “b1”) como la conversión hexadecimal (arriba a la izquierda, en un cuadro dentro del anterior, donde pone “Row” y “Column”).
Para descubrir qué letra es el binario “01101010”, simplemente:
- El número binario para convertir a símbolo ASCII: 01101010
- Quitamos el primer bit (pues no se usa, nos quedamos con los siete últimos): 1101010
- Separamos por posiciones (atendiendo al bit más representativo “MSB”, que es el más a la izquierda y será quien sea el “b7”):
- b7 = 1
- b6 = 1
- b5 = 0
- b4 = 1
- b3 = 0
- b2 = 1
- b1 = 0
- Buscamos el símbolo en la tabla la coincidencia por la fila y la columna: j
Con el hexadecimal es más sencillo:
- El número hexadecimal para convertir a símbolo ASCII: 6A
- Sustituimos los símbolos hexadecimales por decimales: 6 10
- El primer símbolo es “Column” (columna) y el segundo “Row” (fila):
- Column = 6
- Row = 10
- Buscamos el símbolo en la tabla la coincidencia por la fila y la columna: j
Terminar comentando que el hexadecimal se usa para un montón de cosas (aparte de para colores y letras, tal como se comentó), siempre con el motivo de acortar la representación de otras bases inferiores. Para:
- Las direcciones IPs (las que utilizas para conectar un equipo a Internet), sobre todo para el nuevo protocolo IPv6 que soporta 2128 direcciones diferentes. Por ejemplo, una dirección IPv6 podría ser (ya es larga en hexadecimal, imagina en binario): “2001:0DB8:AC10:FE01:2541:FE18:12AE:F81B”
- Las direcciones MAC (la dirección física de la tarjeta de red de cualquiera de tus dispositivos; la “tarjeta de red” es la que identifica tu equipo inequívocamente para ser conectado por ejemplo con un Router, para que tenga Internet). Por ejemplo: “48:6D:43:C2:3C:FE”
- En números de serie de productos. Dependerá del fabricante, pero algunas veces se puede ver hexadecimal en las cajas de productos en vez de en decimal en hexadecimal (como en las cajas de los televisores, microondas, o en las cajas de los Smartphones). También al comprar Software (el número que pide normalmente al instalar, para asegurar que sea original).
- Programar con código ensamblador (el “código ensamblador” se utiliza para programar el procesador de tu ordenador o Smartphone; como, por ejemplo, decir al procesador que sume dos números que están en sendas posiciones de memoria y coloque el resultado en otra posición de memoria). Por ejemplo, una instrucción en código ensamblador puede ser: “C010 B6 80 04”
Octal (base 8)
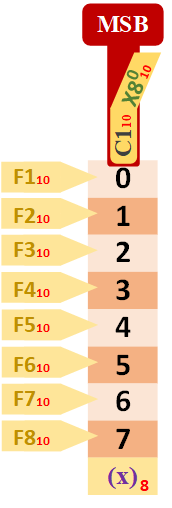
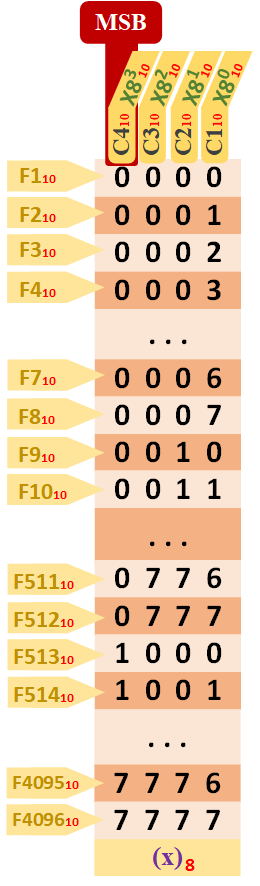
Aunque ya todas las tablas son iguales, no quería terminar sin mostrarte las de octal (base 8 que tiene 8 símbolos: 0, 1, 2, 3, 4, 5, 6, 7), ya que también se usa mucho agrupar el binario en octal (el 8 es una potencia de 2, concretamente: 23=8). No tiene un uso tan extendido como el hexadecimal, pero también es importante. Y se calcula exactamente igual que las otras tablas (aprendida una, todas son iguales).
Rápidamente te enseño la tabla básica de un dígito:
Y otra cualquiera, por ejemplo, la de cuatro dígitos:
También te pongo gratuitamente la comparación de los cuatro sistemas de numeración que hemos visto (binario, octal, hexadecimal y decimal). Para que te fijes que el octal también coincide antes de pasar al siguiente número redondo (“número redondo” me refiero al siguiente del último que acaba la cuenta con los símbolos de un sistema de numeración; es decir, el que termina en “cero”. Para el decimal serían los números redondos el 10, 20, 30,… , 80, 90, 100, etc. Para el binario el: 10, 100, 110, 1000, 1100, 1110, etc. Para el hexadecimal: 10, 20, 30,… , D0, F0, 100, etc. Así como para el octal: 10, 20, 30,… , 60, 70, 100, etc.), exactamente donde también terminan las tablas donde lo hacen el binario y el hexadecimal (como hemos dicho, la coincidencia no es casual, coinciden porque son potencias de 2; el decimal no es potencia de 2, es potencia de 10, y coincidiría con otros sistemas de numeración que sean potencias de 10).
Conversión de octal a decimal
La conversión de octal a decimal igual que los anteriores. Por ejemplo, para convertir el número octal “6017” a decimal:
- El número octal para convertir a decimal: 6017
- Para cada columna su multiplicador decimal: (6 x 83) + (0 x 82) + (1 x 81) + (7 x 80)
- Cada potencia es: (6 x 512) + (0 x 64) + (1 x 8) + (7 x 1)
- Calculamos los paréntesis: 3.072 + 0 + 8 + 7
- Sumamos: 3.087
- Conversión: (6017)8 = (3.087)10
Conversión de octal a binario
Igual de simple que el hexadecimal, para convertir del octal a binario y viceversa:
Convertir de octal a binario. Convertir cada letra del octal a binario por separado. Por ejemplo, convertir el número octal “6701” a binario:
- El número octal para convertir a binario: 6701
- Sustituir cada símbolo hexadecimal por su binario: 110 111 000 001
- Conversión: (6701)8 = (110111000001)2
Conversión de binario a octal
Y al revés igual, convertir de binario a octal. Cada grupo de tres bits es un símbolo octal. Por ejemplo, para convertir el número binario “110111000001” a hexadecimal:
- El número binario para convertir a octal: 110111000001
- Separar en grupos de tres bits: 110 111 000 001
- Sustituir cada grupo por su símbolo hexadecimal: 6701
- Conversión: (110111000001)2 = (6701)8
Conversión del octal a cualquier sistema de numeración
E igual que el hexadecimal, desde el valor en binario podemos convertir el valor a decimal (como vimos anteriormente) o en la base que queramos.
Diferentes significados para un mismo número binario
Depende del programa que abra cada archivo (que tiene bits dentro). Para un programa los bits significaran una cosa y para otro otra.
Por ejemplo, para un programa de edición de imágenes (como el Photoshop o el Gimp) serán posiciones de bits y cada posición tendrá un color (para saber qué pixel pintar y de qué color).
Para un programa reproductor de canciones los bits representarán metadatos (los metadatos es información del audio, como autor de la canción, la duración de la misma, etc.) y la propia señal que reproducirá como audio (la posición de cada punto de la curva de la señal de audio).
O para una calculadora, pues significará un número propiamente o un símbolo con el que operar varios números.
Calculadora on-line:
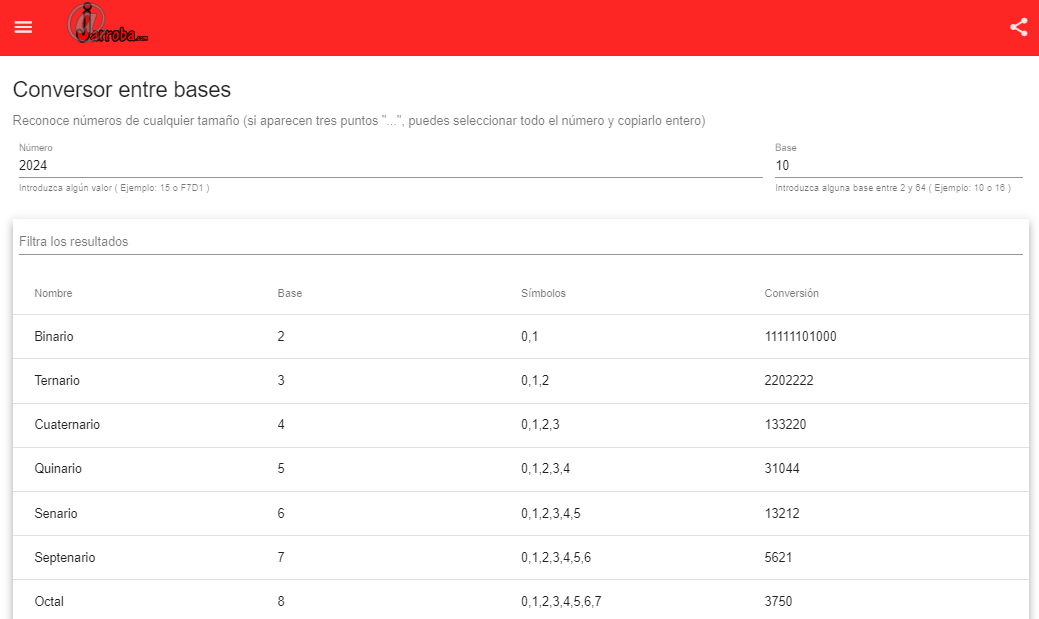
Para convertir cualquier número de una base a cualquier otra podemos utilizar la calculadora online para convertir entre bases. Por ejemplo, para convertir el número «2024» de base 10 (decimal) a cualquier otra base (Ejemplo en: https://jarroba.com/tools/baseconverter/2024/10/%22%22):
Atribuciones
- Imagen del modelo de color RGB del autor Ninja404 obtenida de la Wikipedia: https://upload.wikimedia.org/wikipedia/commons/c/c2/AdditiveColor.svg
- Imagen de gráfico de Código ASCI 1968 del autor LWChris obtenida de la Wikipedia: https://upload.wikimedia.org/wikipedia/commons/archive/8/82/20140820143049%21US-ASCII_code_chart.png
Referencias
- https://es.wikipedia.org/wiki/Sistema_binario
- https://en.wikipedia.org/wiki/Binary_prefix
- https://es.wikipedia.org/wiki/Base_(aritm%C3%A9tica)
- https://es.wikipedia.org/wiki/Sistema_de_numeraci%C3%B3n
- https://es.wikipedia.org/wiki/Base64
- https://en.wikipedia.org/wiki/Unary_coding
- https://es.wikipedia.org/wiki/%C3%8Dndice_(matem%C3%A1tica)
- https://en.wikipedia.org/wiki/Most_significant_bit
- https://en.wikipedia.org/wiki/Least_significant_bit
- https://en.wikipedia.org/wiki/Instruction_set_architecture
- Aparte de la experiencia personal











Muy clara la explicación, muchas gracias!
Bastante clara la manera en que se explicaron los cambios de base y su significado. En lo personal, a mi me sirvió para empezar a agilizar los cálculos mentalmente. Muchas gracias.