Sistema de numeración binario

Para empezar bien y rápido hablando del “binario” te voy a poner un número expresado en el sistema de numeración binario:

0 1 1 0 1 0 1 0

En este mundo digital seguro que -aunque no sepas que significa- te suene la anterior ristra de 0s y 1s (puede que hayas visto números binarios en películas, series, videojuegos, libros o incluso navegando por internet; en algún sitio que exprese algo sobre informática o de ordenadores).

Te pregunto, así sin haber visto más sobre el tema ¿Qué podemos decir del anterior número binario? Si vuelves al número anterior posiblemente pienses “pues tiene 8 bits” (cada estado «1» o «0» es un bit) y “es una secuencia de bits” (en un computador a las secuencias de bits, dependiendo del contexto también se les llama Dato, Trama, Datagrama, Segmento, Instrucciones; muchos nombres, pero de momento solo hace falta que entiendas que una “secuencia de bits” es una ristra de “1s” y “0s”, fácil y sencillo, el resto de nombres los veremos en otros artículos).

El binario se compone de bits (los famosísimos 1s y 0s; toda la información en https://jarroba.com/bit/) y su tamaño se mide con el sistema de unidades de la información (también seguro que has oído hablar de los Megabits o Gigabytes, o de algunos símbolos como Mib, Mb, Gb, GiB, kiB, kB, entre otros muchos; todos en https://jarroba.com/unidades-medida-la-informacion/).

Aunque el binario, como sistema de numeración que es, lo puedes utilizar en tu día de vida normal para por ejemplo contar cosas (sustituyendo al sistema de numeración decimal 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; del que seguro estás ya aburrido 😛 ). En una computadora se utiliza para dos cosas:

Para guardar información. Por ejemplo, guardar una canción (una canción se guarda en binario a nivel de bit en el disco duro de tu dispositivo preferido, dispositivo como tu ordenador, portátil, smartphone, Tablet, etc.).
Para dar órdenes al ordenador (más concretamente llamadas “Instrucciones”). Por ejemplo, reproducir la canción guardada (una orden en binario son bits eléctricos que hacen que el procesador haga una cosa u otra, normalmente más abajo nivel que “reproducir una canción”, como son las operaciones aritméticas tales como sumas binarias o las operaciones lógicas como los famosos AND u OR, control de los datos y operaciones con la memoria como copiar un registro de la memoria a otra parte, etc.).

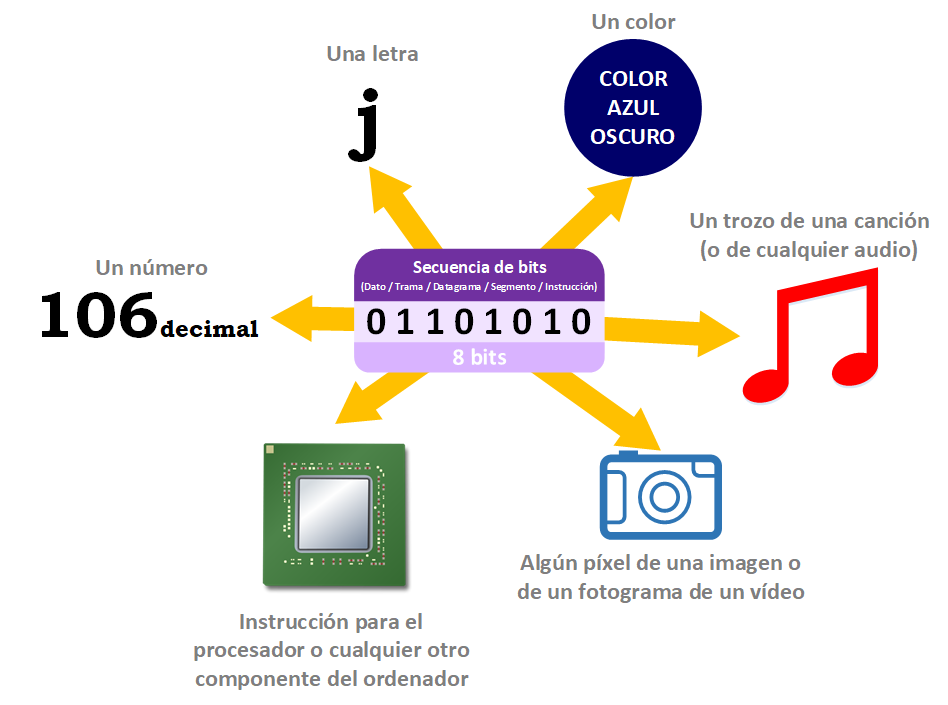
Entonces, si el binario es un sistema de numeración ¿La secuencia binaria “01101010” es un número? Lo es, pero también puede significar otras cosas. Cualquier símbolo que se nos ocurra puede significar cualquier cosa que queramos, por ejemplo, la letra equis “X” es una letra para formar palabras y poder comunicarnos entre humanos, pero también es el símbolo para indicar donde los antiguos piratas enterraban los tesoros, o un número variable para una fórmula matemática (por ejemplo, X+2=4 ), o la marca a la que hay que disparar, o para indicar en un formulario que hemos elegido una casilla; el símbolo “X”, que es una letra y también otras muchas cosas, incluso puede significar lo que quiera que nos inventemos (y como veremos más adelante, «X» también puede significar el número decimal diez «10» ).

¿Entonces “01101010” qué número es? “01101010” es el número “01101010” ¿Si acabamos de decir que puede significar otras cosas? Sí, pero depende del contexto. “01101010 binario” es un número binario que si transformamos al sistema de numeración decimal es el número “106 decimal”, hay que dejar claro desde donde partimos (“01101010 binario”) y hacia dónde vamos (El “106 decimal”) ¿Y cómo se hecho la conversión? No nos adelantemos, primero entender a qué nos referimos por contexto. Y ¿Qué más representa el número binario “01101010”? También el color “azul oscuro” ¿Un color? Sí, también una letra, concretamente la letra “j” (Jota minúscula) ¿Es posible que represente tantas cosas y tan diferentes si “01101010” siempre es “01101010”? Por eso mismo, dependerá del contexto, además podrá significar muchas cosas más (como el símbolo “X” antes comentado).

Este número binario “01101010” también podría representar un sinfín de cosas que te puedas imaginar en un ordenador, como un trozo de una canción o la posición y el color de píxeles de una imagen (o de un fotograma de un vídeo).

Ahora, que te he convencido de todo lo que se puede representar exactamente con el mismo número binario, empezamos con lo divertido, con la ciencia, con la lógica pura, con ¡los números!

Números

Un número binario es un número que se representa con 0s y 1s, pero ¿Porqué representamos el binario con 0s y 1s y no con otros símbolos? Podríamos pensar, el cero es la nada y el uno es algo, por tanto, equivaldría fácilmente a apagado y encendido, lo oscuro y la luz, el mal y el bien, la nada y el algo, entre otros muchos temas más filosóficos. Sin embargo, no es así, poco tiene que ver con el “apagado” y “encendido”, o la “nada” y “algo”, más bien como “ocurre algo” u “ocurre otra cosa diferente” (la curiosidad es muy grande, y si la tienes en el artículo de bit vimos que un bit se represente con «0» o «1» tan solo indica estados diferentes en momentos puntuales de un bit). Entonces ¿Porqué se escogieron los símbolos «0» y «1»? Porque ya teníamos símbolos que podíamos reutilizar con los que estamos más que acostumbrados (y no tener que inventar otros).

Los símbolos de los números decimales que estamos acostumbrados a utilizar: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (cada uno de estos símbolos se llama «dígito» o «cifra»). Se cree que los números se inventaron en China, luego llegaron a la India sobre el siglo V, donde saltaron a Oriente medio aproximadamente en el año 670, y cuando los árabes llegaron a la península ibérica se arraigaron por ser convenientes y desde entonces son los que se utilizan, denominándose por esto “números arábigos” (o “guarismos”) porque provienen de Oriente Medio. Luego vino la reconquista española (en el año 722 España echó a los árabes; más información de la reconquista en https://es.wikipedia.org/wiki/Reconquista ) y se continuaron utilizando los números arábigos (era algo útil y ya muy usado, no había motivo para eliminar dichos símbolos). Se extendieron por Europa en la Edad Media, y luego con las colonizaciones Europeas al continente Americano y al resto del mundo se terminó de universalizar su uso (más información de los números arábigos en https://es.wikipedia.org/wiki/N%C3%BAmeros_ar%C3%A1bigos ).

Todas las culturas de nuestro planeta -la Tierra- representaban los números de una forma u otra. Como por ejemplo, los egipcios con jeroglíficos (más información de números egipcios en https://es.wikipedia.org/wiki/Numeraci%C3%B3n_egipcia ), pero su sistema que era decimal se perdió, no nos llegó (lo que sí nos llegaron fueron “los números arábigos” que utilizamos).

También los famosos números romanos, representan cantidades con símbolos que agrupaban múltiplos de uno y cinco (Incluso todavía hoy se utilizan en algunos relojes, para numerar siglos como “siglo XXI”, o para contar nombres de reyes iguales sucesivos como “Alfonso X”).

Hasta en la misma Prehistoria (hace unos 20.000 años) se representaba cada unidad con un palo vertical, y la quinta tachaba cuatro palos verticales para agrupar en múltiplos de cinco (Más información en https://es.wikipedia.org/wiki/Cuenta_(matem%C3%A1ticas) ).

Era muy casual que culturas tan diferentes, agruparan sus números de cinco en cinco o de diez en diez, por lo que se supone que inventaron nuestros antepasados diez números porque contamos con los diez dedos de la mano (de pequeños contamos con los dedos, e incluso de mayores para ciertos cálculos nos ayudamos de ellos).

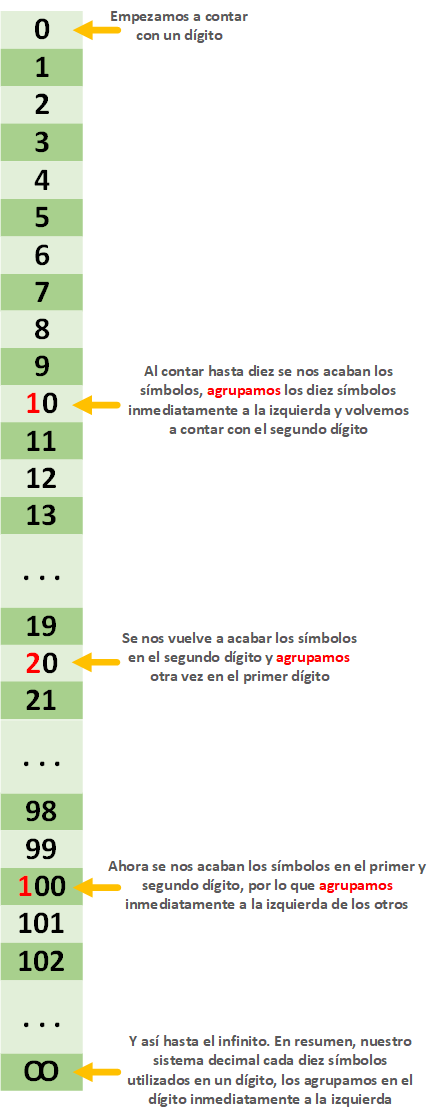
Llega el momento presente, nacemos nosotros y nos enseñan los “números arábigos”, son sencillos porque son diez números y cada uno se presenta por un símbolo diferente. Y aquí llega la confusión, pensamos siempre en múltiplos de diez («10»), que es el sistema decimal que utiliza como símbolos de la numeración arábiga (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Cada diez cosas contadas con estos símbolos se realiza una agrupación y se reinicia la cuenta. Es decir, contamos de la siguiente manera:

Entonces, si utilizamos un sistema decimal, es lógico suponer que existan otros sistemas de numeración como los siguientes (a continuación, verás muchos números, no hace falta aprenderse todo, pero sí que nos suenen y conocer dónde recordar la información; tienes el recordatorio tanto en esta web como en otros muchos sitios gratuitamente y a tu entera disposición 🙂 ):

El binario: que solo tiene dos símbolos que lo representen (los símbolos elegidos para este sistema de numeración son el 0 y el 1)
El ternario: con tres símbolos (0, 1, 2)
El cuaternario: con cuatro símbolos (0, 1, 2, 3)
El quinario: con cinco símbolos (0, 1, 2, 3, 4)
El octal: con ocho símbolos (0, 1, 2, 3, 4, 5, 6, 7)
El decimal: con diez símbolos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
El hexadecimal: con dieciséis símbolos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Donde la letra es igual a un número decimal: A=10, B=11, C=12, D=13, E=14, F=15. Escribir estas letras en mayúscula o minúscula representa al mismo número, es decir “B=b”)
El trigesimal: con treinta símbolos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T. Donde la letra es igual a un número decimal: A=10, B=11, …, S=28, T=29. Escribir estas letras en mayúscula o minúscula representa al mismo número).
El base 32: con treinta y dos símbolos (A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z, 2, 3, 4, 5, 6, 7. Donde la letra es igual a un número decimal y el símbolo de los números representa otros números decimales diferentes: A=0, B=1, …, Y=24, Z=25, 2=26, 3=27, …, 6=30, 7=31. Escribir estas letras en mayúscula o minúscula representa al mismo número).
El base 64 (Un sistema de números curioso y muy empleado en informática, para codificar cualquier cosa, como una imagen o una canción en letras y números): con sesenta y cuatro símbolos (la convención elegida cambia un poco de orden al de los anteriores, pero la idea es la misma y me gusta porque se pasa de los símbolos normales de números arábigos y abecedario varias veces y hay que estar utilizando letras mayúsculas y minúsculas -en esta base “B” mayúscula es un número diferente que “b” minúscula- así como otros dos símbolos que dependerán del protocolo, como el de suma “+” y la barra lateral “/”. Generalmente los símbolos elegidos en orden son: A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z, a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, /)

Nota sobre el “trigesimal” y otros “-al”::

El “trigesimal” me lo he “medio inventado”, pues no es tan usado, pero lo quería poner para que tuvieras con que comparar. Realmente sí existe o es susceptible de existir, como existe el “vigesimal” de 20 símbolos, el “tetragesimal” de 40, el “Pentagésimal” de 50, el “Pentatrigesimal” de 35, el “Centoctopentagesimal” de 158, pero no se usan tan extendidamente como los otros en informática (solo unos pocos sistemas de numeración se utilizan en conjunto con el binario) que incidiremos en este artículo. Lo he añadido porque necesitamos de otro ejemplo con el que comparar al “hexadecimal” (muy utilizado junto al binario, como veremos). Para la anterior base 32 se nombraría como «Duotrigesimal» y para la base 64 como «Tetrahexagesimal».

La tabla completa de la representación lingüística para el nombre de los sistemas de numeración referidos a la informática (tabla gracias a la RAE):

1: Unario
2: Binario
3: Ternario
4: Cuaternario
5: Quinario
6: Senario
7: Septenario
8: Octal
9: Nonario
10: Decimal
11: Undecimal
12: Duodecimal
13: Tridecimal
14: Tetradecimal
15: Pentadecimal
16: Hexadecimal
17: Septemdecimal
18: Octodecimal
19: Nonadecimal
20: Vigesimal
21: Unvigesimal
22: Duovigesimal
23: Trigesimal
…

Para las decenas:

10: Decimal
20: Vigesimal
30: Trigesimal
40: Tetragesimal
50: Pentagesimal
60: Hexagesimal
70: Septemgesimal
80: Octogesimal
90: Nonagesimal

Para las centenas:

100: Centesimal
200: Duocentesimal
300: Tricentesimal
400: Tetracentesimal
…

Los símbolos a utilizar podrían ser cuales quiera: los números arábigos, los jeroglíficos egipcios, la numeración romana, los palos de conteo de la Prehistoria, símbolos extraterrestres, símbolos que nos inventemos cada uno en nuestras casas, etc. Como queremos universalizar el sistema (al fin y al cabo, sirve para comunicarnos entre los humanos y es algo básico), se ha estandarizado el uso de números arábigos para contar del cero al nueve en cualquier sistema de numeración (salvo algunos casos). Y para sistemas de numeración que requieran más de diez símbolos, se utilizan otros símbolos también muy utilizados, el mismísimo abecedario (A, B, C, D, E, …).

Te he contado toda esta historia, para entender la realidad de los números con ello escapar del Matrix creado alrededor del sistema decimal (para cambiar la percepción habitual de que solo existe del cero al nueve, y que los símbolos arábigos se reutilizan para otros sistemas de numeración, así como el abecedario u otros símbolos), y ahora para entender las propiedades del sistema binario junto con las diferentes representaciones para cada sistema de numeración.

Base

Ahora una gran duda ¿Cómo sabemos en que sistema de numeración está por ejemplo el número “101”? Parece claramente que es binario, pero si nos detenemos un segundo a analizarlo descubrimos que también podría ser ternario (el ternario utiliza también símbolo 0 y el 1, como vimos arriba), o por lo mismo podría ser quinario (que también utiliza los símbolos 0 y 1), octal o decimal, hexadecimal, trigesimal o base 64. Es decir, este número, podría estar expresado en cualquier sistema de numeración.

Otro número, por ejemplo, el “97”, sí que queda claro que no es binario (pues el binario solo tiene los símbolos «0» y «1», por lo que lo descartamos), tampoco puede ser ni ternario, ni quinario, ni octal por lo mismo; sí que podría ser del decimal en adelante cualquier otro sistema de numeración.

La base no es otra cosa que el número de símbolos con el que cuenta un sistema de numeración:

El binario: base 2 (porque tiene «dos» símbolos, el 0 y el 1)
El ternario: base 3 (porque tiene «tres» símbolos, el 0, el 1, y el 2)
El cuaternario: base 4
El quinario: base 5
El octal: base 8
El decimal: base 10
El hexadecimal: base 16
El trigesimal: base 30
El base 32: base 32
El base 64: base 64

Por otro lado, se puede decir tanto “este número es binario” o “este número es base 2”, que significa lo mismo. Igual para todos los sistemas de numeración (el “base 64” directamente no tiene un nombre “extra ordinal” como bien pudiera ser “sexagésimocuarternario”, se nombra siempre como “base 64”, la base es su propio nombre y se dice directamente “este número es base 64”; aunque tampoco estaría mal decir “sexagésimocuarternario”, solo por pereza de decir una palabra tan larga 🙂 ).

Como hemos visto antes con el ejemplo del número “101”, necesitamos una forma de diferenciar los sistemas de numeración, y para ello utilizamos la llamada “base” que es en esencia escribir el número de la base en pequeño a la derecha (un subíndice) del número entre paréntesis (Por ejemplo, para decir que el número “101” es binario, lo escribimos con su base “(101)₂”). Con esto diferenciamos de qué sistema de numeración estamos hablando.

Más ejemplos rápidos para cada base:

El binario: (101)₂, (101110101)₂
El ternario: (101)₃, (1021222)₃
El cuaternario: (101)₄, (311021)₄
El quinario: (101)₅, (340143)₅
El octal: (101)₈, (47165142730)₈
El decimal: (101)₁₀, (7046815392)₁₀
El hexadecimal: (101)₁₆, (A8B3DF97310CD)₁₆
El trigesimal: (101)₃₀, (1ACJQ97R80DTG)₃₀
El base 32: (101)₃₂, (RG2EOGW4LD576FGO)₃₂
El base 64: (101)₆₄, (sdHf7Gg+94DVra/E1fas)₆₄

Nota sobre los subíndices: A veces se puede ver sin paréntesis (por ejemplo, ver el número “(101)₂” como “101₂”), esto no es correcto en bastantes casos, pues crea confusión sobre todo con variables. Por ejemplo, para la variable “x”, no es lo mismo decir “(x)₂” que “x₂”; “(x)₂” quiere decir que el número que sea “x” es binario, mientras que “x₂” representa a uno de los números de una sucesión (x₁ x₂ x₃ … x_n). Sin embargo, “101” no es una variable por lo que no lleva a confusión utilizar “101₂” en vez de “(101)₂” (personalmente prefiero utilizar los paréntesis, opino que es más efectivo y óptimo aprender el estándar universal).

¿Existe un sistema de numeración de base 1, un sistema “unario”? Es decir ¿El sistema binario acaso no es el más pequeño?:

El sistema unario existe y hemos comentado un ejemplo, el de los palos de la Prehistoria que solo tiene un único símbolo: el palo. Cada vez que se ponía un palo ( | ), ya se agotaban los símbolos existentes, por lo que había que poner otro para representar la siguiente cantidad ( || ), y otro más para la siguiente ( ||| ), y así hasta el infinito.

Hoy día se utiliza el “código unario” para enviar datos sin pérdidas (a través de Internet, por ejemplo), para comprimir datos sin pérdidas, para el entrenamiento de redes neuronales, entre otras cosas. Utilizando el símbolo “1” (recuerda que no es un 1 decimal, se escogió el símbolo “1” posiblemente porque se parece a un palo, se podría haber escogido cualquier otro símbolo del “5” o “%” por ejemplo; además, donde se utiliza este “código unario” en informática es en bits que trabajan sobre un sistema binario). Donde “1” en unario es un 1 en decimal, “11” es 2 en decimal, “111” es 3 en decimal, y así con los que queramos. Como se utiliza sobre bits (1 bit tiene dos estados, es un sistema binario), se utiliza el “1” binario como “1” unario y el “0” binario como separador de los grupos de los “1s” unarios (por ejemplo, el número unario “111011011111” sería en decimal 325); e incluso, a veces se usa al revés, el “0” como símbolo unario y el “1” como separador.

Y como se puede esperar, el unario es base 1 y se representa con el subíndice 1, por ejemplo: (11111)₁

Curiosidad de un sistema de base 60 antiguo:

No quería terminar esta parte sin contarte una curiosidad más. Antes, cuando te conté la historia de los números, mencioné que antiguamente utilizarían los dedos para ayudarse en las cuentas y por eso ahora tenemos el sistema decimal. Pues la antigua Mesopotamia contaba en base 60 (tenía sesenta símbolos para su sistema de numeración), y ellos también utilizaban los dedos para contar, pero con las falanges de los dedos (si miras a la palma de una de tus manos podrás comprobar como cuatro dedos se dividen en tres partes por las líneas donde se dobla el dedo, y el dedo gordo no se utilizaba para contar; con lo que se usaban 12 falanges de una mano, sin usar las falanges del gordo, y con la otra mano se levantaban los 5 dedos para agrupar de 12 en 12, con lo que 12×5 = 60. Más información de este sistema sexagesimal en https://es.wikipedia.org/wiki/Sistema_sexagesimal )

Ya hemos aprendido todo lo que teníamos que saber relativo a los números. Y este artículo trata sobre “binario”, por lo que nos quedamos solo con los sistemas numéricos que nos interesan y los más utilizados en informática que son: el binario (normal que sea el que nos interesa, es de lo que va el artículo 😉 ), el octal, el hexadecimal, el base 64 (vamos a ir viendo para qué los queremos, pues están muy relacionados con el binario), y el decimal (realmente este no nos interesa tanto, pero partiremos de lo que entendemos de este sistema de numeración para entender el resto).

Representaciones

Hemos visto como se representan las bases en los diferentes sistemas de numeración de manera “general” (en matemáticas), pero no como los vas a ver habitualmente en informática (sobre todo si programas). A continuación, te muestro rápidamente otras representaciones (algunas convenciones son de algunos lenguajes de programación como de C, aunque está bastante extendido su uso), y más ejemplos con la base para que sirvan como referencia:

Binario: Se antepone “0b” (cero y la letra “b”) al número, o se pone una “B” mayúscula al final, o se pone de subíndice “bin”
- 0b00011010
- 00011010B
- 00011010bin
- (00011010)₂
Octal: Se antepone “0o” (cero y la vocal “o”) al número, o se pone de subíndice “oct”
- 0o17824783
- 17824783oct
- (17824783)₈
Decimal (los símbolos de puntuación de separación de miles, como pudiera ser “894.632.190.648”, no se ponen al programar): Se representa sin nada delante, o se pone una “D” al final, o se pone de subíndice “dec”
- 894632190648
- 894632190648D
- 894632190648dec
- (894632190648)₁₀
Hexadecimal: Se antepone “0x” (cero y la letra “x”) al número, o se pone una “H” mayúscula al final (que estén las letras que significan número en mayúscula o minúscula no importa en hexadecimal), o se pone de subíndice “hex”, también se puede ver precedido por la almohadilla “#”:
- 0xAE45782D
- ae45782dH
- AE45782Dhex
- #AE45782D
- (AE45782D)₁₆
Base 32:
- (34RZO7LE5BFS)₃₂
Base 64:
- (5IGNDh+cm5yhbCBw/DVra)₆₄
- Ninguno, uno “=” o dos “==” símbolos igual al final del número (por ejemplo: dHJhc2dhcw== ): aunque ayudan a diferenciar estos números, no es una manera de representación pues son caracteres de relleno (un “=” indican 8 bits vacíos, dos “==” son 16 bits vacíos; es decir, si aparecen los símbolos igual “=” es que el número es más corto de lo que debe; por ejemplo algunos protocolos es obligatorio que el número base 64 sea múltiplo de 24 bits, así si el número ocupa 8 bits se añadirán dos iguales “==”, si ocupa 16 bits se añadirá un igual “=”, y si ocupa 24 bits no se añade ningún símbolo igual)

Si sientes más curiosidad de como funciona el binario, te recomiendo que eches un vistazo al siguiente artículo de combinaciones y conversiones desde y hacia el binario pinchando aquí.

Agradecimientos

Artículo dedicado especialmente a Jorge Moraleda, quien fue mi profesor de matemáticas en el colegio Obispo Perelló. Durante las clases siempre nos deleitaba con curiosidades sobre los números, curiosidades que eran más que interesantes y conseguían mantenernos atentos, tanto que todavía hoy me acuerdo después de tantos años.

Atribuciones

«Tabla de la representación lingüística de los nombres de los sistemas de numeración» ofrecido por la «Real Academia Española» como respuesta a consulta.