Selección del número óptimo de Clusters
- El proyecto de este post lo puedes descargar pulsando AQUI.
- Este post forma parte del libro "Machine Learning (en Python), con ejemplos"
Uno de los problemas que nos encontramos a la hora de aplicar alguno de los métodos de Clustering (K-means o EM) es la elección del número de Clusters. No existe un criterio objetivo ni ampliamente válido para la elección de un número óptimo de Clusters; pero tenemos que tener en cuenta, que una mala elección de los mismos puede dar lugar a realizar agrupaciones de datos muy heterogéneos (pocos Clusters); o datos, que siendo muy similares unos a otros los agrupemos en Clusters diferentes (muchos Clusters).
Aunque no exista un criterio objetivo para la selección del número de Clusters, si que se han implementado diferentes métodos que nos ayudan a elegir un número apropiado de Clusters para agrupar los datos; como son, el método del codo (elbow method), el criterio de Calinsky, el Affinity Propagation (AP), el Gap (también con su versión estadística), Dendrogramas, etc. Dada la complejidad de alguno de estos métodos, vamos a explicar aquellos que son más sencillos y que nos dan; para la mayoría de los casos, unos resultados que nos permiten tomar la decisión de cuál será el número optimo de Clusters para el conjunto de datos. Estos métodos serán el método del codo, los Dendrogramas y el Gap.
La implementación de los métodos mencionado se encuentran implementados en el siguiente repositorio:
https://github.com/RicardoMoya/OptimalNumClusters
Para poder ejecutar estos scripts es necesario tener instaladas las librerías de numpy, matplotlib, scipy y scikit-learn. Para descargar e instalar (o actualizar a la última versión con la opción -U) estas librerías; con el sistema de gestión de paquetes pip, se deben ejecutar los siguiente comandos:
pip install -U numpy pip install -U matplotlib pip install -U scipy pip install -U scikit-learn
Método del codo (Elbow Method)
Este método utiliza los valores de la inercia obtenidos tras aplicar el K-means a diferente número de Clusters (desde 1 a N Clusters), siendo la inercia la suma de las distancias al cuadrado de cada objeto del Cluster a su centroide:
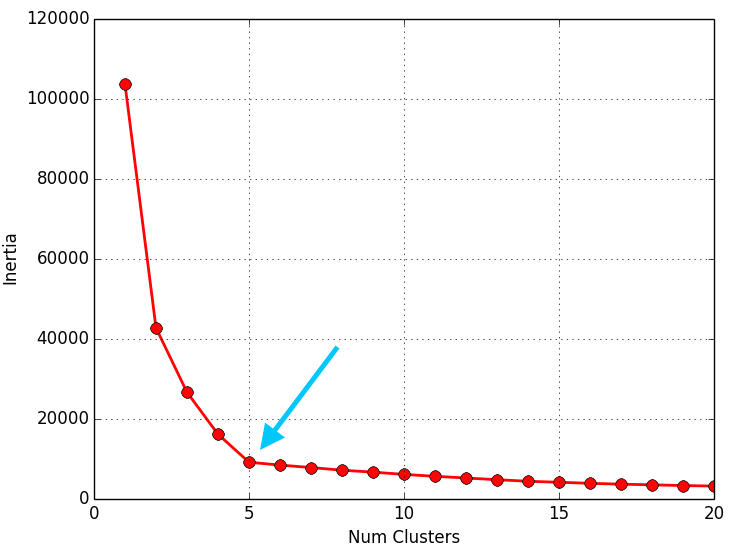
Una vez obtenidos los valores de la inercia tras aplicar el K-means de 1 a N Clusters, representamos en una gráfica lineal la inercia respecto del número de Clusters. En esta gráfica se debería de apreciar un cambio brusco en la evolución de la inercia, teniendo la línea representada una forma similar a la de un brazo y su codo. El punto en el que se observa ese cambio brusco en la inercia nos dirá el número óptimo de Clusters a seleccionar para ese data set; o dicho de otra manera: el punto que representaría al codo del brazo será el número óptimo de Clusters para ese data set.
El script que se muestra a continuación, calcula los valores de la inercia tras aplicar el K-means de 1 a 20 Clusters (para uno de los 3 data sets que tenemos) y los pinta en una gráfica lineal (número de Clusters respecto a la inercia) para poder apreciar “el codo” y por tanto determinar el número optimo de Clusters para el data set:
# -*- coding: utf-8 -*-
__author__ = 'RicardoMoya'
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
# Constant
DATASET1 = "./dataSet/DS_3Clusters_999Points.txt"
DATASET2 = "./dataSet/DS2_3Clusters_999Points.txt"
DATASET3 = "./dataSet/DS_5Clusters_10000Points.txt"
LOOPS = 20
MAX_ITERATIONS = 10
INITIALIZE_CLUSTERS = 'k-means++'
CONVERGENCE_TOLERANCE = 0.001
NUM_THREADS = 8
def dataset_to_list_points(dir_dataset):
"""
Read a txt file with a set of points and return a list of objects Point
:param dir_dataset:
"""
points = list()
with open(dir_dataset, 'rt') as reader:
for point in reader:
points.append(np.asarray(map(float, point.split("::"))))
return points
def plot_results(inertials):
x, y = zip(*[inertia for inertia in inertials])
plt.plot(x, y, 'ro-', markersize=8, lw=2)
plt.grid(True)
plt.xlabel('Num Clusters')
plt.ylabel('Inertia')
plt.show()
def select_clusters(dataset, loops, max_iterations, init_cluster, tolerance,
num_threads):
# Read data set
points = dataset_to_list_points(dataset)
inertia_clusters = list()
for i in range(1, loops + 1, 1):
# Object KMeans
kmeans = KMeans(n_clusters=i, max_iter=max_iterations,
init=init_cluster, tol=tolerance, n_jobs=num_threads)
# Calculate Kmeans
kmeans.fit(points)
# Obtain inertia
inertia_clusters.append([i, kmeans.inertia_])
plot_results(inertia_clusters)
if __name__ == '__main__':
select_clusters(DATASET1, LOOPS, MAX_ITERATIONS, INITIALIZE_CLUSTERS,
CONVERGENCE_TOLERANCE, NUM_THREADS)
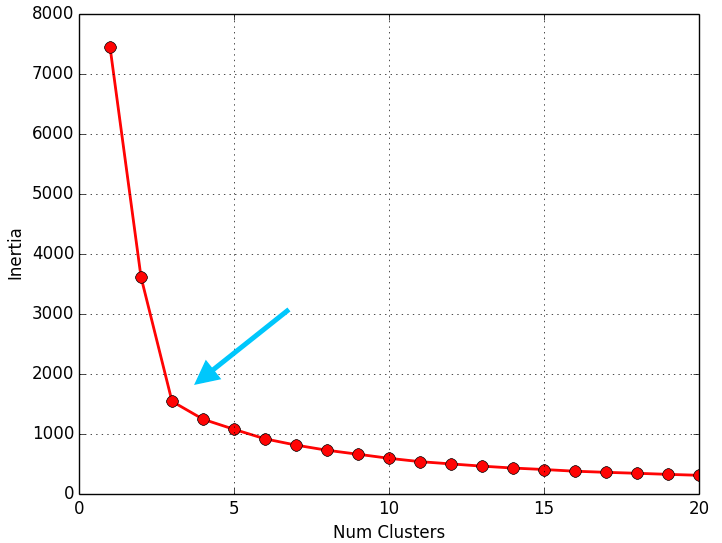
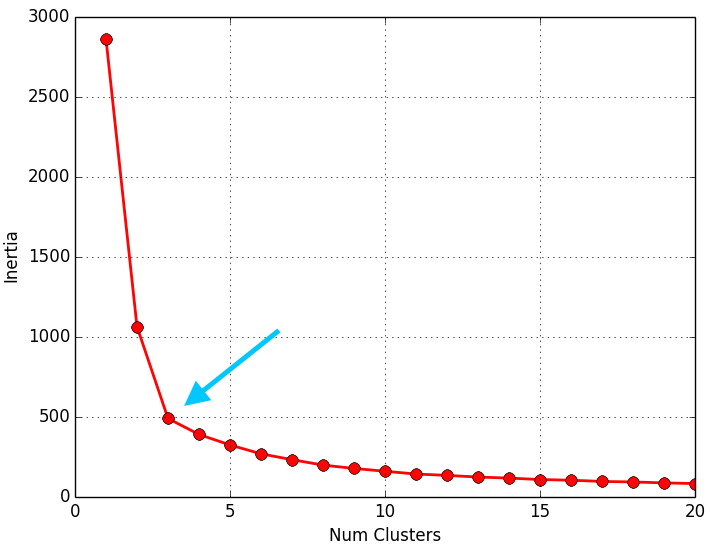
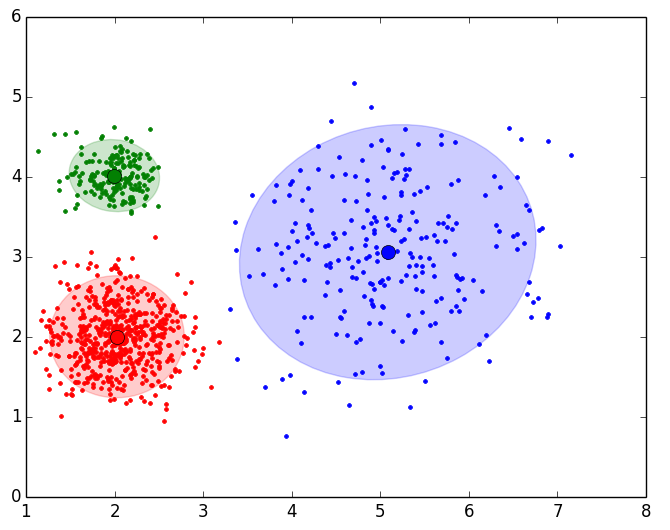
A continuación se muestran los resultados obtenidos para cada uno de los tres data sets. El script solo devuelve la gráfica lineal. La representación de los Clusters que se muestra al lado de la gráfica lineal se ha obtenido con el script que implementa el EM y se muestran para poder apreciar que el número de Clusters que nos indica el método del codo es coherente:
Como se puede apreciar en los resultados obtenidos, el método del codo devuelve unos valores muy coherentes y se ajusta a los resultados esperados. Es posible que al aplicar este método para otro conjunto de datos no se aprecie “el codo” o incluso se observen dos o más codos (o cambios bruscos en la evolución de la inercia). En ese caso habría que estudiar más en detalle o con otras técnicas el número optimo de Clusters a seleccionar. Dada la finalidad didáctica de estos ejemplos, se aprecia muy bien “el codo” en la evolución de la inercia, pero en la realidad no siempre se observa este comportamiento tan claro.
Dendrogramas
Un dendrograma es un tipo de representación gráfica en forma de árbol que organiza y agrupa los datos en subcategorías según su similitud; dada por alguna medida de distancia. Los objetos similares se representan en el dendrograma por medio de un enlace cuya posición está determinada por el nivel de similitud entre los objetos o grupos de objetos. Dadas estas características, hace que los dendrogramas sean un tipo de diagrama muy útil para estudiar las agrupaciones de objetos; es decir, para estudiar los Clusters que pueden darse en un data set.
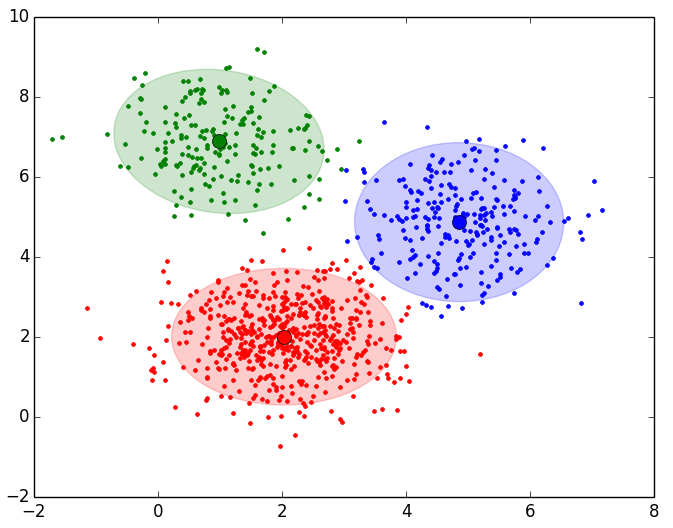
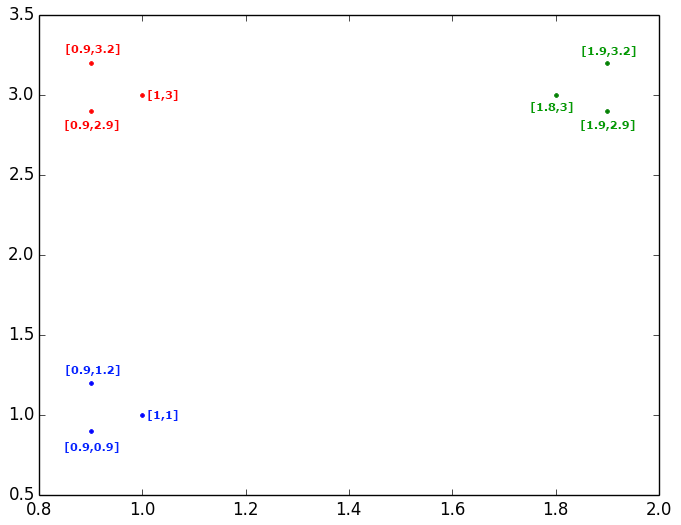
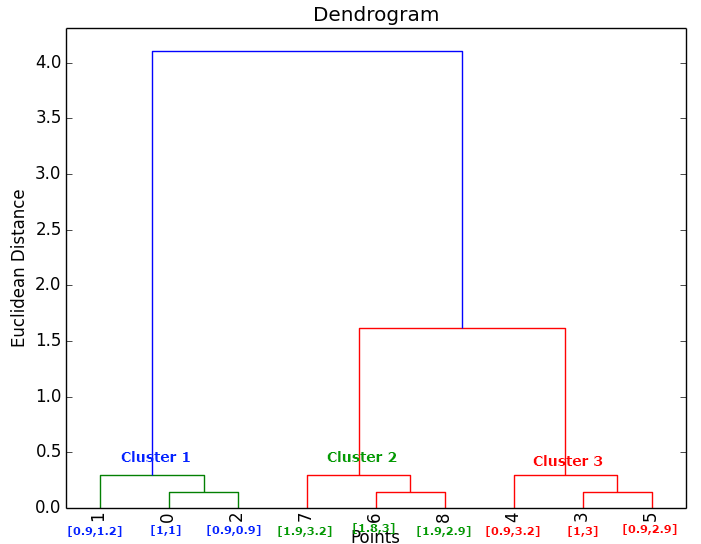
Veamos a continuación un sencillo ejemplo, en el que tenemos 9 objetos representados en un plano:
Se puede observar claramente que estos 9 objetos los podemos agrupar en 3 Clusters, pero comencemos estudiando las similitudes y distancias entre objetos. En primer lugar fijémonos en los objetos de color azul y veamos las distancias (euclideas en este caso) entre esos objetos. Vemos que los dos puntos más cercanos entre sí son el punto {1,1} y el punto {0.9,0.9}, por lo que los uniríamos en el dendrograma con un enlace. Si agrupamos estos dos puntos y calculamos su centroide, obtenemos el punto {0.95,0.95} y este nuevo punto tiene como punto más cercano de entre todos los que hay en el plano al punto {0.9,1.2}; por tanto, uniríamos con otro enlace al primer grupo formado, con el punto {0.9,1.2}. En resumen lo que se hace es calcular la distancia entre todos los puntos, cogemos la menor distancia, agrupamos esos dos puntos, y volvemos a calcular la distancia entre todos los puntos o entre todos los grupos ya formados y puntos.
Siguiendo estos pasos, el dendrograma resultante para estudiar la relación entre los 9 puntos antes mostrados sería el siguiente, dando lugar a interpretar que el número optimo de Clusters a seleccionar serian 3:
El script que se muestra a continuación calcula con el método linkage() las relaciones entre los puntos y grupos más similares, representando estos resultado en un dendrograma al cual hemos limitado el nivel de detalle de las agrupaciones hasta que muestre en su nivel más bajo 12 grupos de objetos:
# -*- coding: utf-8 -*-
__author__ = 'RicardoMoya'
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage
# Constant
DATASET1 = "./dataSet/DS_3Clusters_999Points.txt"
DATASET2 = "./dataSet/DS2_3Clusters_999Points.txt"
DATASET3 = "./dataSet/DS_5Clusters_10000Points.txt"
def dataset_to_list_points(dir_dataset):
"""
Read a txt file with a set of points and return a list of objects Point
:param dir_dataset:
"""
points = list()
with open(dir_dataset, 'rt') as reader:
for point in reader:
points.append(np.asarray(map(float, point.split("::"))))
return points
def plot_dendrogram(dataset):
points = dataset_to_list_points(dataset)
# Calculate distances between points or groups of points
Z = linkage(points, metric='euclidean', method='ward')
plt.title('Dendrogram')
plt.xlabel('Points')
plt.ylabel('Euclidean Distance')
# Generate Dendrogram
dendrogram(
Z,
truncate_mode='lastp',
p=12,
leaf_rotation=90.,
leaf_font_size=12.,
show_contracted=True
)
plt.show()
if __name__ == '__main__':
plot_dendrogram(DATASET1)
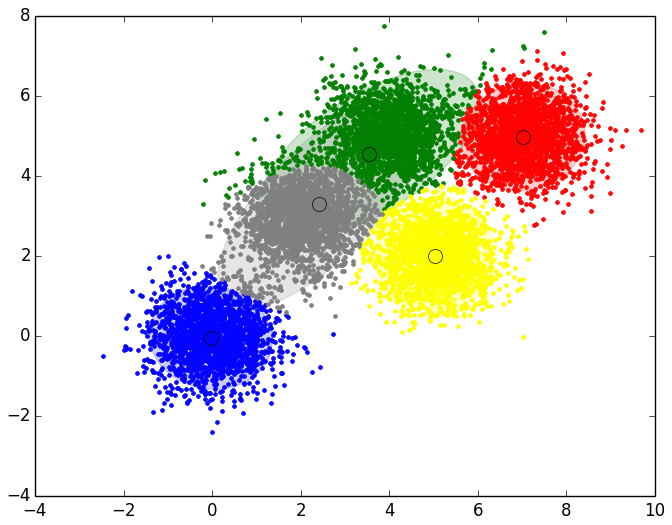
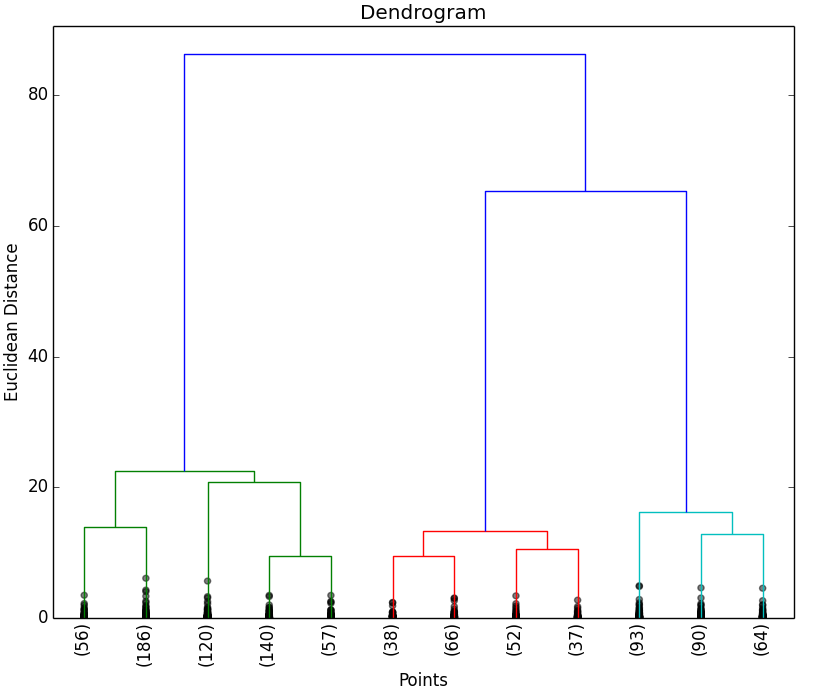
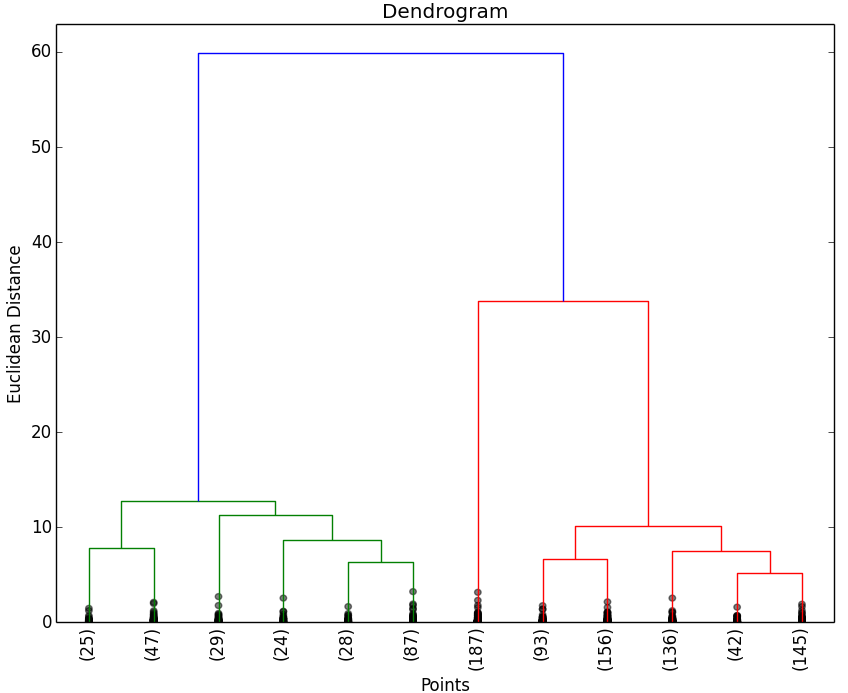
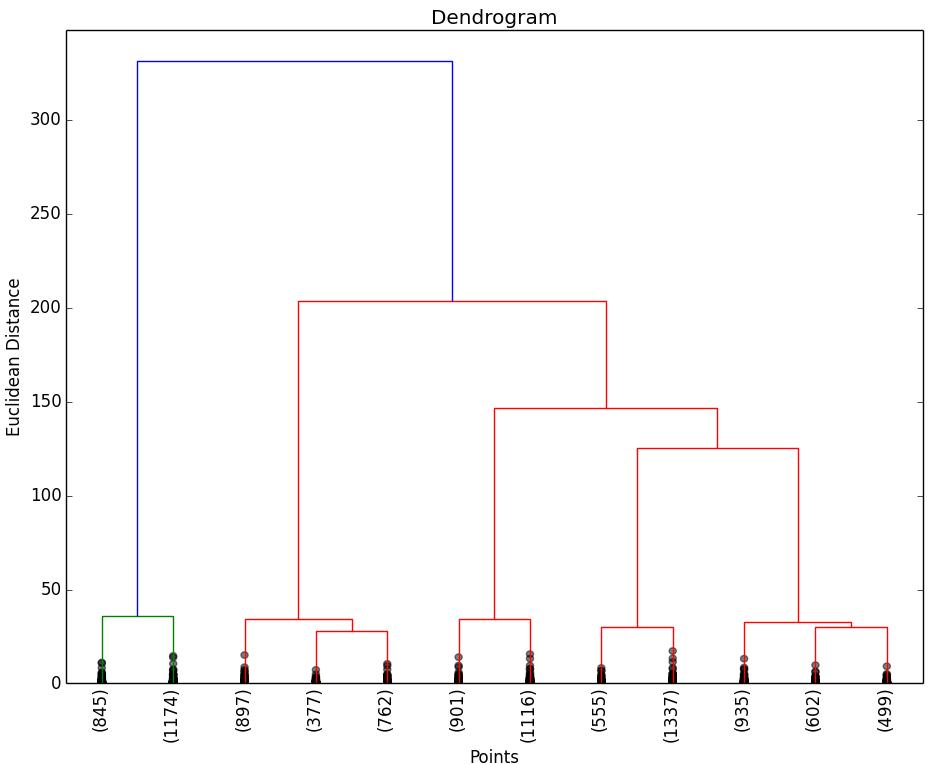
A continuación se muestran los resultados obtenidos para cada uno de los tres data sets. El script solo devuelve el dendrograma. La representación de los Clusters que se muestra al lado del dendrograma se ha obtenido con el script que implementa el EM y se muestran para poder apreciar que el número de Clusters que nos indica el dendrograma.
Como puede observarse en los resultados obtenidos, los dendrogramas muestran las agrupaciones (Clusters) de objetos esperados. Al igual que en la aplicación del método del codo, es posible que no se puedan apreciar claramente las agrupaciones de objetos, por lo que habría que estudiar con otras técnicas el número óptimo de Clusters a seleccionar.
Gap
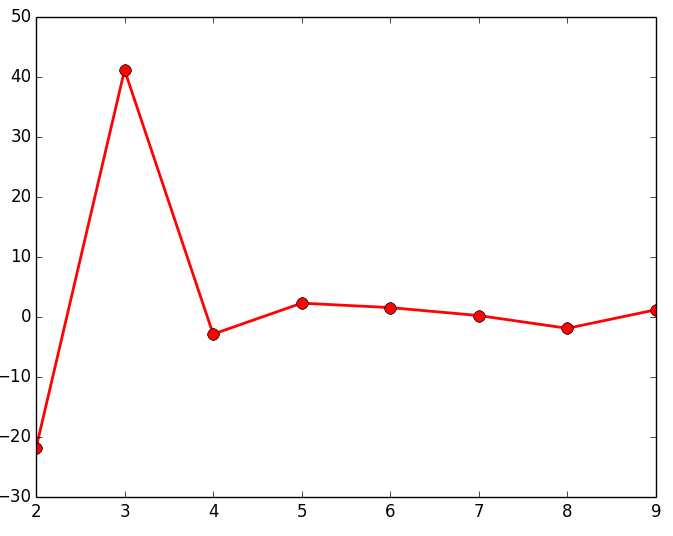
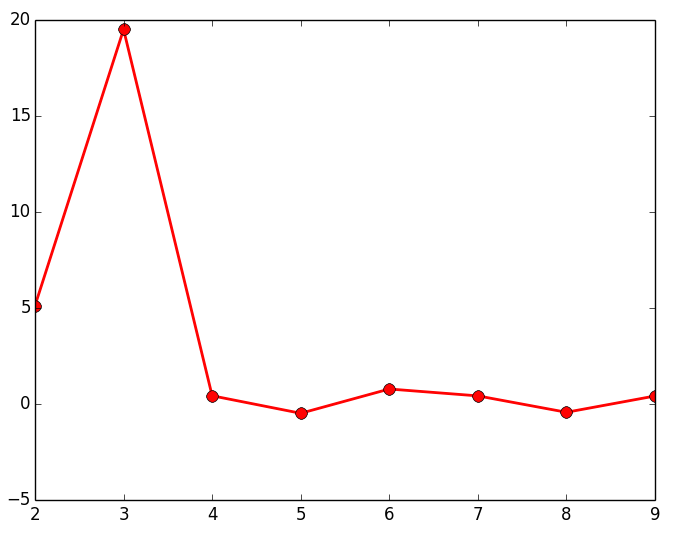
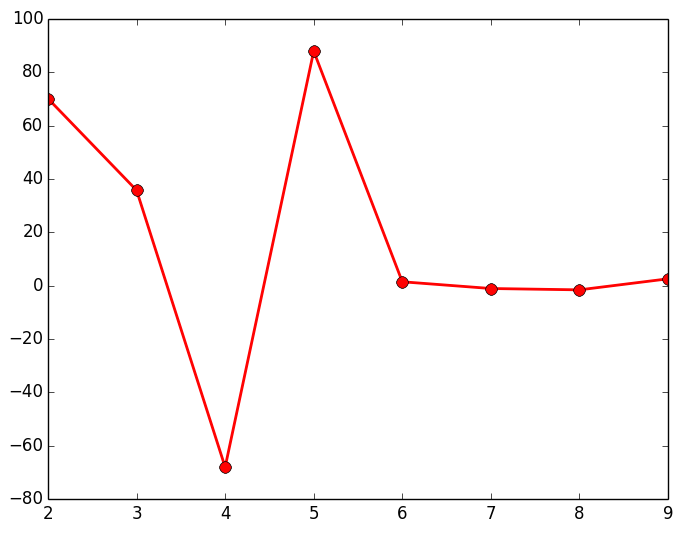
El último de los métodos que vamos a mostrar es el Gap (brecha); similar al método del codo, cuya finalidad es la de encontrar la mayor diferencia o distancia que hay entre los diferentes grupos de objetos que vamos formando para representarlos en un dendrograma. Para ello vamos cogiendo las distancias que hay de cada uno de los enlaces que forman el dendrograma y vemos cual es la mayor diferencia que hay entre cada uno de estos enlaces. El script que se muestra a continuación calcula estas diferencias (para alguno de los 3 data sets de los que disponemos) y las representa en una gráfica lineal, siendo el punto máximo, el número de Clusters optimo para ese data set.
# -*- coding: utf-8 -*-
__author__ = 'RicardoMoya'
import numpy as np
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import linkage
# Constant
DATASET1 = "./dataSet/DS_3Clusters_999Points.txt"
DATASET2 = "./dataSet/DS2_3Clusters_999Points.txt"
DATASET3 = "./dataSet/DS_5Clusters_10000Points.txt"
def dataset_to_list_points(dir_dataset):
"""
Read a txt file with a set of points and return a list of objects Point
:param dir_dataset:
"""
points = list()
with open(dir_dataset, 'rt') as reader:
for point in reader:
points.append(np.asarray(map(float, point.split("::"))))
return points
def plot_gap(dataset):
points = dataset_to_list_points(dataset)
# Calculate distances between points or groups of points
Z = linkage(points, metric='euclidean', method='ward')
# Obtain the last 10 distances between points
last = Z[-10:, 2]
num_clustres = np.arange(1, len(last) + 1)
# Calculate Gap
gap = np.diff(last, n=2) # second derivative
plt.plot(num_clustres[:-2] + 1, gap[::-1], 'ro-', markersize=8, lw=2)
plt.show()
if __name__ == '__main__':
plot_gap(DATASET1)
A continuación se muestran los resultados obtenidos para cada uno de los tres data sets. El script solo devuelve la gráfica lineal. La representación de los Clusters que se muestra al lado de la gráfica lineal se ha obtenido con el script que implementa el EM y se muestran para poder apreciar que el número de Clusters que nos indica la gráfica.
Como puede observarse en los resultados obtenidos estudiando el gap, devuelve el número de agrupaciones (Clusters) esperados. Al igual que en el resto de métodos mostrados anteriormente, es posible que no se puedan apreciar claramente las agrupaciones de objetos, por lo que habría que estudiar con otras técnicas el número óptimo de Clusters a seleccionar.
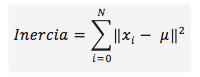

Hola Ricardo,
Estoy realizando un análisis cluster para mi TFG y me ha servido mucho tu articulo. Te lo agradezco mucho que lo hayas compartido. Tengo una pregunta sobre el código: ¿Cual es el motivo por el que utilizas Loops=20, max_iterations=10, tolerancia de convergencia=0.001 y Num_threads=8?
Un saludo y gracias de nuevo.
Hola Alex.
Algunas te tus preguntas las puedes sacar del siguiente artículo donde explico algunas de ellas.
Sobre los parámetros que me comentas te respondo:
– Loops=20: Lo que hago con este parámetro es calcular la inercia para ‘K’ Clusters y ver el codo. Con este loop calculo la inercia desde 2 a 20 Clusters. En este caso he puesto 20 como podia haber puesto 10, 15 o 25, simplemente es para ver el cambio brusco de tendencia en la inercia que este se da para 3, 5 o 7 clusters dependiendo del ejemplo.
– Los parámetros de max_iterations, tol y n_jobs los puedes ver en la documentación de sklearn: https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html.
-max_iterations: es el número de veces que se hace la asignación y actualización (una iteración) de clusters
-tol: es un parámetro para parar el algoritmo del k-means (una condición de parada); es decir, definimos primeramente el max_iterations y supongamos que en vez de poner 10 ponemos 1000. Como hacer el proceso de asignación y actualización 1000 veces tarda mucho y es costoso, ese parámetro lo que indica es que si al hacer una iteración la inercia cambian menos de ese valor entre un loop y otro se para la ejecución. Por ejemplo si vamos por la iteración 23 y vemos que la inercia de la iteración 23 difiere menos del umbral indicado de la iteración 22, el algoritmo deja de ejecutar iteraciones y no realiza las 977 iteraciones restantes.
-Num_threads: es el número de cores que usará el proceso para ejecutarse. Si no le indicas nada utilizará todos los cores que tu sistema operativo le permita y si no utilizará el número de cores que le indiques (si es que los tiene.